Expresse a integral como uma integral iterada de seis modos diferentes, onde é o sólido limitado pelas superfícies dadas.
Passo 1
Falaa, pessoal!
Nessa questão precisamos expressar uma integral de seis formas diferentes...
Como assim??!
Bom, lembra que em uma integral tripla a gente integra em função de , , e , e sempre integramos de dentro pra fora, seguindo a ordem dos diferenciais que aparecem no final da integral:
Essa ordem pode ser feita de seis formas diferentes, que no fundo é a permutação desses três diferenciais (se você não lembra de análise combinatória, não se assusta, que a gente não vai precisar usar aqui 😅).
Aqui a gente vai precisar usar o conceito de regiões dos tipos , e :
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
- Região do tipo é quando o está entre duas funções de e , onde é a projeção da região no plano .
Uma integral sobre uma região do tipo é calculada assim:
Sendo que esse pode ser ou .
A integral fica:
E o é ou
Nesse caso, a integral é:
Com o sendo ou
Percebeu que pra cada um dos três tipos de região nós temos duas formas de escrever a integral? Então, essas vão ser as seis formas de escrever!
Pra determinar todas elas, a gente vai descrever nossa região como dos tipos , e , e escrever as formas associadas a cada um deles!
Eu sei que parece muita coisa, mas vamos aos poucos!
Passo 2
(1) Região do tipo
As superfícies que limitam o sólido são
é o plano , e é um paraboloide elíptico.
Pra achar a interseção das duas é só igualar o das duas equações:
O que é uma elipse no plano .
Vamos desenhar isso tudo:
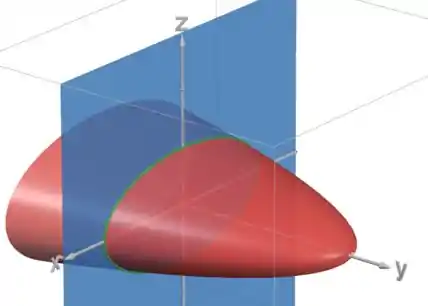
Em vermelho temos o paraboloide, em azul o plano e em verde a interseção.
O sólido fica assim:
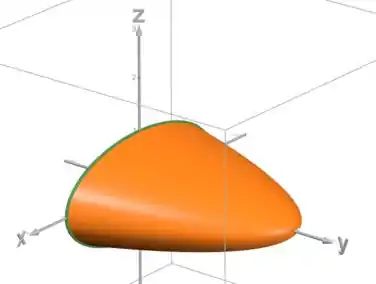
Primeiro vamos descrever esse sólido como uma região do tipo . Então precisamos que esteja entre duas funções de . Pra isso, vamos isolar o na equação da superfície:
Tirando a raiz, chegamos em dois resultados:
A primeira equação representa a parte da superfície que está acima do plano (onde ), e a segunda é a parte abaixo. Como nosso sólido está entre essas duas partes da superfície:
Passo 3
Com relação a e , vamos ver a projeção do sólido no plano .
Ela é limitada pela interseção do paraboloide com o próprio plano :
E pelo plano
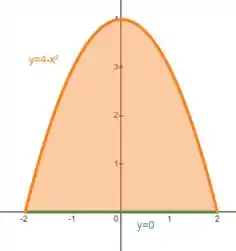
A forma mais direta de definirmos os limites aqui é:
O está entre a reta e a curva :
E o está entre e :
Então temos todos os limites das variáveis:
Percebe que com esses limites, a integral tem que ser feita exatamente nessa ordem , já que os limites de dependem de e os limites de dependem de .
Assim chegamos na nossa primeira integral:
Para inverter a ordem desse , precisamos voltar para o plano , e reescrever a curva
Isolando :
Essas duas equações representam a parte esquerda e direita da curva:
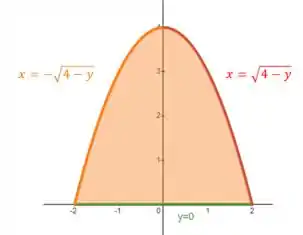
E agora podemos escrever que:
E:
Então:
E achamos a segunda forma da integral!
Passo 4
(2) Região do tipo
Agora vamos enxergar o sólido como uma região do tipo :
Pra isso, precisamos isolar o na equação do paraboloide:
Tirando a raiz, chegamos em dois resultados:
Analogamente ao que a gente fez em (1), nossa região está entre essas duas equações:
Passo 5
Para os limites de e , vamos ver a projeção no plano , que é limitada pela interseção do paraboloide com esse plano:
E pelo plano
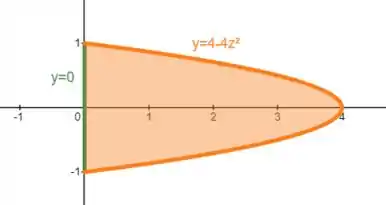
Como está entre essa parábola e a reta :
E varia de até .
Então já temos os limites das variáveis:
De novo, pela dependência dos limites, temos que escrever a integral nessa ordem :
Para inverter , vamos isolar o na equação:
Na projeção:
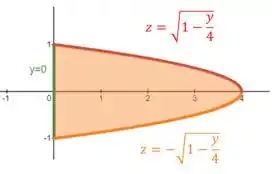
Então escrevemos:
E a integral:
E já temos quatro integrais! Só faltam duas!!
Passo 6
(3) Região do tipo
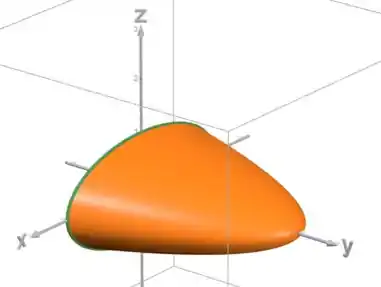
Pra escrever o sólido como uma região do tipo , vamos voltar pro nosso desenho:
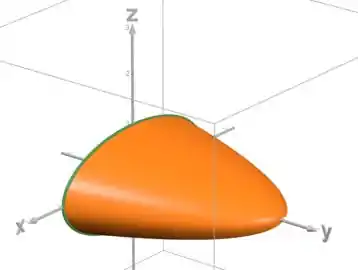
O sólido está entre o plano e o paraboloide da seguinte forma:
Então temos que:
Passo 7
Pra acharmos os limites de e vamos ver a projeção no plano .
O limite dessa projeção é a elipse verde, que já calculamos:
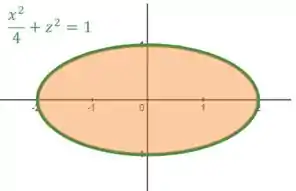
Agora, tem duas formas da gente descrever esses limites (que vão ser as duas últimas integrais).
A primeira é isolando o nessa equação:
Que são a parte de cima e de baixo da elipse:
E:
Juntando com os limites de :
Temos a integral:
A última forma é isolando o na equação da elipse:
Que são as partes da direita () e da esquerda () da elipse, então:
E:
E finalmente temos a nossa última integral:
Ufaaa, acabamos! 😪