Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 3
A figura mostra um retângulo inscrito em um triângulo isósceles cuja hiponetuna tem unidades de comprimento:
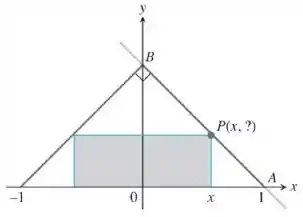
Expresse a ordenada de em termos de
Expreswse a área do retângulo em termos de
Qual a maior área possível para o retângulo? Quais são as suas dimensões?
Passo 1
Letra
A nossa figura é essa:
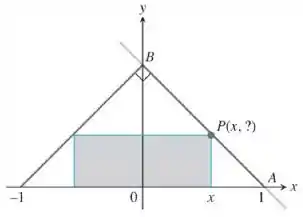
Vamos começar achando a coordenada de .
Ele disse que esse triângulo é isósceles e retângulo, então o ângulo em é
Como está no eixo , vamos ter que o triângulo é retângulo em , que é a origem do eixo cartesiano.
Assim, o ângulo em desse triângulo vai ser também, fazendo ser isolsceles e
Logo as coordenada de será:
Passo 2
As coordenadas de são aquelas da reta que passa por e por .
Sua equação vai ser
Passando em e
Vamos ter:
Terminando com:
A reta fica:
Então as coordenadas de são:
Passo 3
Letra
A área vai ser:
Onde a base do retângulo vale e a altura
Com indo de até .
Passo 4
Letra
Para achar a maior área possível, temos que achar o ponto de máximo de .
Para isso, temos que ver se existe algum extremo no intervalo de e comparar com os extremos do intervalo.
Vamos começar achando a derivada:
Ela vai ser em:
Passo 5
Achamos o nosso ponto crítico. Vamos usar o teste da segunda derivada para conferir se ele é máximo ou mínimo ou nada rs
Como a segunda derivada deu negativo, é um ponto de máximo.
Passo 6
Vamos comparar agora os valores de em
Então vamos ter que a área máxima é .
Vamos achar as dimensões do retângulo.
Fazendo
Logo é um retângulo por
Resposta
Letra
Letra
Letra