Mostre que entre todos os retângulos tendo um perímetro de 36 cm, o quadrado com 9 cm de lado tem a maior área.
Passo 1
Seja o retângulo dado abaixo:
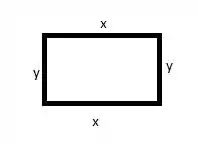
Por hipótese temos que seu perímetro é igual a 36. Assim:
(1)
Passo 2
A área deste retângulo será dada por:
(2)
De (1) temos:
Substituindo em (2) temos:
Como agora depende somente da variável podemos reescrever:
Note que, como e são medidas de lados do retângulo, devemos ter e . Assim:
Logo, temos .
Passo 3
Derivando a equação da área temos:
Como é uma equação polinomial, temos que essa derivada existe para todo valor de . Desta forma, os pontos críticos de ocorrem quando . Assim:
Note que:
Se , temos ;
Se , temos .
Assim, pelo teste da primeira derivada temos um máximo de em .
Substituindo em (1) temos:
Portanto, o retângulo de perímetro 36 cm e com maior área é o quadrado de lado 9 cm, como queríamos mostrar.
Resposta
Ei, a resposta está no passo a passo :)