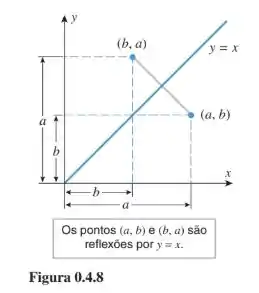
A Figura é uma “prova por imagens”de que a reflexão do ponto pela reta é o ponto . Demonstre isso rigorosamente com os passos seguintes.
- Prove que, se não estiver na reta , então e são distintos e a reta por e é perpendicular à reta
- Prove que, se não estiver na reta então o ponto médio do segmento está na reta
- Explique cuidadosamente o significado geométrico de refletir pela reta .
- Use os resultados das partes para provar que é a reflexão de pela reta
Passo 1
-
Vamos tratar não estando na linha e em outro ponto. Queremos provar que o segmento de reta é perpendicular a reta
A inclinação da linha e a inclinação do segmento .
Dessa forma o segmento de e o segmento Atestando a perpendicularidade.
Passo 2
Nós vamos provar que o ponto médio no segmento está na linha Considerando que e não estão alinhados. O ponto médio do segmento deve ser , dessa forma o ponto médio consegue estar na linha . Se:
Passo 2
(c)
Geometricamente, é reflexo de sobre alinha e isso significa que o segmento de reta está sobre a linha , e o segmento de reta será perpendicular a linha e o ponto médio está na linha
Passo 3
(d)
Para provar que é a reflexão de olhamos o ponto médio que está acima da linha e que o segmento de reta é perpendicular a linha Isso significa que é reflexão de .
Resposta
Ei, a resposta está no passo a passo :)