5.
a. Mostre que e são inversas uma da outra.
b. Esboce em um único gráfico e em um intervalo de suficientemente grande para mostrar o cruzamento de ambos em e . Certifique-se de que o gráfico apresenta a simetria necessária em relação à reta .
c. Determine os coeficientes angulares das tangentes aos gráficos de e em e (quatro tangentes no total).
d. Quais retas tangenciam as curvas na origem?
Passo 1
a.
Para provar que é a inversa de é bem fácil, podemos pegar a função e aplicar a raiz cubica dos dois lados da equação:
Portanto a inversa de é igual a :
Passo 2
b.
Os dois gráficos são simples de desenhar por serem bastante conhecidos. O primeiro uma função do terceiro grau e o segundo uma função raiz cubic.
Podemos plotar alguns pontos, para termos um gráfico mais fiel. E vamos obter:
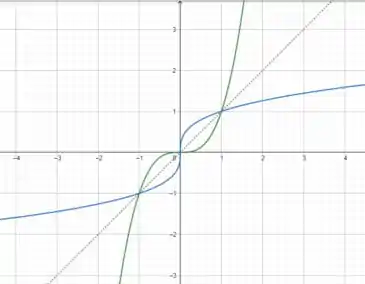
A linha pontilhada é a linha , podemos observar que as funções apresentam a simetria necessária.
Passo 3
c.
O coeficiente angular da tangente, em certo ponto da função, é a derivada da função naquele ponto.
Então vamos calcular a derivada das funções e :
e
Passo 4
c.
Agora só precisamos achar o valor das derivadas nos pontos dados:
No ponto :
e
No ponto :
e
Passo 5
d.
Essa é fácil, é só observarmos o gráfico que vamos ver que a reta tangente à em é:
Mas se você fez um esboço do gráfico e não tem certeza é só derivar e alpicar a derivada nesse ponto:
E para é a mesma coisa. A gente observa no gráfico que a reta tangente em irá ser:
E podemos calcular usando a derivada também:
Acontece que não podemos dividir por zero, então imagine que o x está tendendo a zero. Nesse caso está tendendo ao infinito, uma reta com o coeficiente angular infinito é uma reta na vertical, ou seja, a reta tangente a curva nesse ponto é a reta .
Resposta
b.
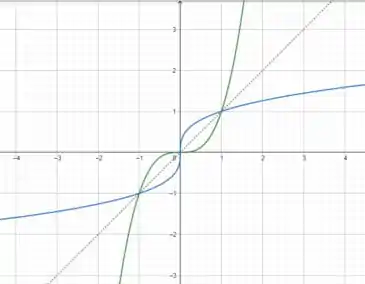
c. No ponto :
No ponto :
d.
Para :
Para :