Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 30

A figura a seguir mostra um círculo de raio r com uma corda de comprimento 2 e um arco s de comprimento 3 . Use o método de Newton para resolver   r e θ (radianos) com quatro casas decimais. Suponha que 0   < θ   < π .

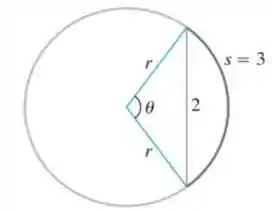
Passo 1

Utilizando o método de Newton para aproximação de raízes que nos diz que

x n + 1 = x n - f ( x n ) f ' ( x n )

Queremos encontrar um valor para r e para θ , para isso vamos tentar colocar uma variável em função da outra para facilitar os cálculos.

Passo 2

Da geometria do problema podemos escrever que θ = s r . Se tomarmos a bissetriz do ângulo central θ e desenharmos o seguinte triângulo retângulo

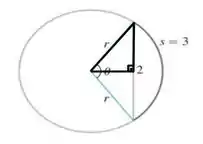
Temos que s e n θ 2 = 1 r , como nosso θ = 3 r podemos substitui-lo e vamos obter

s e n θ 2 = 1 r

s e n 3 r 2 = 1 r

s e n 3 2 r = 1 r

Agora, queremos saber quais valor(es) de r satisfazem a igualdade e para isso tomemos a seguinte função

f r = s e n 3 2 r - 1 r

Assim poderemos aplicar o método de Newton e para isso, vamos derivar nossa função f r obtendo

f ' r = - 3 2 r 2 ⋅ cos ⁡ 3 2 r + 1 r 2

Passo 3

Temos, então, todas as ferramentas para resolver o problema basta, então, substituirmos os valores na fórmula do método de Newton

r n + 1 = r n - s e n 3 2 r n - 1 r n - 3 2 r n 2 ⋅ cos ⁡ 3 2 r n + 1 r n 2

Tomando r 0 = 1 vamos obter

r 0 + 1 = r 0 - s e n 3 2 r 0 - 1 r 0 - 3 2 r 0 2 ⋅ cos ⁡ 3 2 r 0 + 1 r 0 2

r 1 = 1 - s e n 3 2 - 1 1 - 3 2 ⋅ 1 2 ⋅ cos ⁡ 3 2 + 1 1 2

r 1 = 1 - s e n 3 2 - 1 - 3 2 ⋅ cos ⁡ 3 2 + 1

r 1 = 1 , 00280

Repetindo esse procedimento utilizando o termo anterior vamos obter

r 2 = 1,0028 2

r 3 = 1,0028 2

Assim, poderemos aproximar r ≈ 1.0028 e obteremos θ

θ = 3 r

θ = 3 1.0028   ≈ 2.9916

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores aproximados de r 1 a r 4 na fatoração 8 x 4-14 x 3-9 x 2+11 x-1=8 ( x-r1) ( x-r 2 ) ( x-r 3 ) ( x–r 4 )
Use o método de Newton para determinar as raízes de f ( x )=4 x 4-4 x 2 usando os valores iniciais fornecidos. x o=- 2 e x o=- 0,8 , situadas em - ∞ ,- 2 2 x 0=-0,5 e x 0=0,25 , situadas em - 21 7 , 2
O retângulo apresentado na figura possui um lado no eixo y positivo, um lado no eixo x positivo e seu vértice superior direito na curva y = e - x 2 . Que dimensões dão ao retângulo a maior área possív
Encontrar as dimensões de um retângulo que possui um lado no eixo x , um lado adjacente a esse no eixo y , o vértice em comum a esses lados na origem e o vértice oposto a ele na curva y = ln ⁡ x x 2 ,
Nos exercícios 21 e 22, obtenha uma aproximação de π com cinco casas decimais, usando o Método de Newton para resolver a equação.