Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 127

O retângulo apresentado na figura possui um lado no eixo y positivo, um lado no eixo x positivo e seu vértice superior direito na curva y = e - x 2 . Que dimensões dão ao retângulo a maior área possível, e qual é essa área?

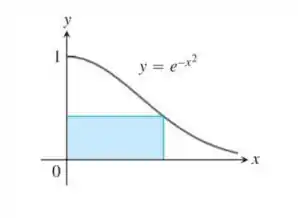
Passo 1

Para o vértice genérico pertencente a curva, temos as coordenadas:

( x , e - x 2 )

Portanto, a expressão da área A do retângulo é dada por:

A = x . e - x 2

Passo 2

A fim de maximizar a expressão da área, vamos derivar e igualar a zero:

A ' = x . e - x 2 ' = 1 . e - x 2 + x . - 2 x . e - x 2 = 0

e - x 2 1 - 2 x 2 = 0

x 2 = 1 2

x = 2 2

Tendo o valor de x, podemos encontrar o valor de y:

y = e - 1 2 = 1 e

Passo 3

Logo, o valor da maior área possível é:

A = 2 2 . 1 e = 1 2 e = 0,43   u . a .

Resposta

x = 2 2

y = 1 e

A = 1 2 e = 0,43   u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Será c o s3 x igual a x para algum x ? Justifique sua resposta.Use o método de Newton para determinar onde isso ocorre.
Para que valor(es) de x obteremos c o s( x ) =2 x ?
Explique por que as quatro questões seguintes pedem a mesma informação: Determine as raízes de f ( x )=x 3-3 x-1 . Determine as abscissas da interseção da curva y=x 3 com a reta y=3 x+1 . Determine as
Use o método de Newton para determinar a quarta raiz positiva de 2 resolvendo a equação x 4-2=0 . Comece com x 0=1 e calcule x 2 .
Quantas soluções a equação s e n( 3 x )=0,99-x 2 possui?Use o método de Newton para determiná-las.