Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 16.Exercícios práticos - Ex. 2

A figura a seguir mostra três caminhos poligonais que ligam a origem ao ponto ( 1,1 , 1 ) . Integre f x , y , z = x 2 + y - z sobre cada caminho.

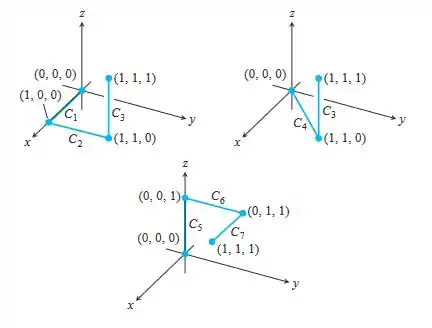
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Caminho 1 – Primeiramente, nós podemos definir que para todo ( x , y , z ) em C 1 , x = y = 0 , com o intervalo sendo 0 ≤ z ≤ 1 , portanto,

∫ f   d s = ∫ 0 1 f x , 0,0   d x = ∫ 0 1 x 2   d x = x 3 3 0 1 = 1 3

Para C 2 , x = 1 ,   z = 0 e o intervalo 0 ≤ y ≤ 1 ,

∫ f   d s = ∫ 0 1 f 1 , y , 0   d y = ∫ 0 1 ( 1 + y )   d x = y + y 2 2 0 1 = 3 2

E para C 3 , temos x = y = 1 e 0 ≤ z ≤ 1 , com isso

∫ f   d s = ∫ 0 1 f 1 , 1 , z   d z = ∫ 0 1 2 - z d z = 2 z - z 2 2 0 1 = 2 - 1 2 = 3 2

Portanto, a integral de linha ao longo do caminho 1 é:

∫ f   d s = 1 3 + 3 2 + 3 2 = 10 3

Passo 2

Caminho 2 - nós podemos definir que para todo ( x , y , z ) em C 4 , z = 0 , com o intervalo sendo 0 ≤ x = y ≤ 1

r 4 t = t i + t j ,     0 ≤ t ≤ 1

E o módulo

r 4 ' t = i + j = 2

Assim, a integral de linha ao longo deste segmento é

∫ f d s = ∫ 0 1 t 2 + t 2   d t

Que tem como resultado

∫ f   d s = 2 t 3 3 + t 2 2 0 1 = 5 6 2

Portanto, a integral de linha ao longo do caminho 2 é:

∫ f   d s = 5 2 6 + 3 2 = 5 2 + 9 6

Passo 3

Caminho 3 - definindo que para todo ( x , y , z ) em C 5 , x = y = 0 , que percorre o segmento,

∫ f   d s = ∫ 0 1 f 0 , 0 , z   d z = ∫ 0 1 - z   d z = - z 2 2 0 1 = - 1 2

Para C 6 , x = 0 ,   z = 1 e o intervalo 0 ≤ y ≤ 1 ,

∫ f   d s = ∫ 0 1 f 0 , y , 1   d y = ∫ 0 1 ( y - 1 )   d y = y 2 2 - y 0 1 = 1 2 - 1 = - 1 2

E para C 7 , temos 0 ≤ x ≤ 1 e y = z = 1 , com isso

∫ f   d s = ∫ 0 1 f x , 1 , 1   d x = ∫ 0 1 x 2 + y - 1 d z = x 3 3 0 1 = 1 3

Portanto, a integral de linha ao longo do caminho é dado por:

∫ f   d s = - 1 2 + 1 3 - 1 2 = - 2 3

Resposta

C a m i n h o   1 :   ∫ f   d s = 10 3

C a m i n h o   2 :   ∫ f   d s = 5 2 + 9 6

C a m i n h o   3 :   ∫ f   d s = - 2 3

Exercícios de Livros Relacionados

Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = 1 + x y e x yi → + x 2 e x y j → C : r t = cos ⁡ ti + 2s e ntj , 0 ≤ t ≤ π 2
4. Calcule ∫ C F ⋅ dr → Ondef. Fx , y , z = y z , x z , x y + 1 e C é a fronteira do triangulo de vértices 0,0 , 0 ,1,1 , 1 ,- 1,1 , - 1 percorrida nessa ordem
Determine se a afirmação é falsa ou verdadeira. Se for verdadeira, explique por quê. Caso contrário, explique por que ou dê um exemplo que mostre que é falsaSe F for um campo vetorial, então rot F é u
Integre f (x , y , z) = sqrt(x^2 + z^2) sobre a circunferência r (t) = (a cos t) j + (a sen t) k , 0 = t = 2 pi