Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 53
Uma firma de embalagem necessita fabricar caixas retangulares de 64 cm³ de volume. Se o material da parte lateral custa a metade do material a ser usado para a tampa e para o fundo da caixa, determinar as dimensões da caixa que minimizam o custo.
Passo 1
Beleza galera, vamos olhar esta caixa mais de perto:
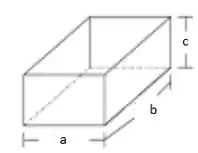
A tampa e o fundo possuem área igual a ab, enquanto a lateral é ac e bc.
Neste caso nós temos um problema de otimização restrita, ou seja, queremos encontrar o valor mínimo para o custo, mas sabendo que o volume deve ser igual a 64 cm³.
Então neste caso a condição será:
Agora precisamos montar a função a ser minimizada, ok? Supondo que o valor do material da tampa e do fundo é , então o valor do material das laterais será .
Agora podemos laçar a função do custo total:
Reorganizando:
Então, nós teremos o seguinte problema de otimização:
Passo 2
Colocando na fórmula de Lagrange:
Derivando L em relação às variáveis a, b e c e igualando as derivadas a zero:
Igualando as duas primeiras equações nós achamos:
Multiplicando a terceira equação por 2 e igualando com a segunda, achamos:
Colocando na última equação:
Achando y e z:
Sendo assim, nós temos o ponto .
Gostaram?