Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.5 - Ex. 89
Se for contínua em , demonstre que
Para o caso onde e , faça um diagrama para interpretar geometricamente essa equação como uma igualdade de áreas.
Passo 1
Diremos que , então .
Passo 2
Sendo assim, temos
Passo 3
Diagrama:
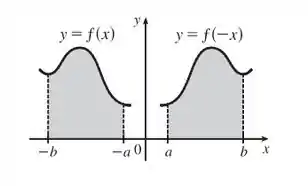
Pelo diagrama, nós vemos que a equidade se segue do fato de que nós estamos refletindo o gráfico de e os limites da integração pelo eixo .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre as integrais nos Exercícios 17-66. ∫ d y arctan y 1 + y 2
Calcule as integrais nos Exercícios 69 e 70. ∫ sin θ θ cos 3 θ d θ
Se você não souber qual substituição fazer, tente reduzir a integral passo a passo, usando uma primeira substituição para simplificar um pouco a integral e depois outra para simplificar um pouco mais.
Efetue a antidiferenciação: ∫ c o s x 2 + s e n x 5 d x
Efetue a antidiferenciação: ∫ yc o s e c 3 y 2 c o t g 3 y 2 d y