Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 41
Se for crescente em um intervalo , segue da Definição que com qualquer do intervalo . Use esse resultado nesses exercícios.
Mostre que se e confirme a desigualdade com algum recurso gráfico computacional. [Sugestão: Mostre que é crescente em .]
Passo 1
Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, precisamos usar as definições e usos das derivadas. Para o caso em questão, temos a sugestão dada para verificar o comportamento da função e ver se ela é crescente ou não.
Usando a derivada, a função é crescente se a sua derivada resultar em um valor maior que dentro de um intervalo aberto.
Passo 2
Então, através da inequação dada
Conseguimos colocar os termos de um lado apenas da equação para obter:
E seguindo a sugestão mostrada no enunciado, podemos verificar se essa função é crescente em um intervalo e, a partir da Definição , comprovar a relação da desigualdade.
Passo 3
Dessa forma, derivando a função:
Vemos que a função é crescente para todos os valores , porque sua derivada é maior ou igual a zero para o intervalo .
Com esse resultado e com a Definição , podemos concluir que:
Visto que:
Então, se , essa inequação pode ser reescrita como:
Portanto:
Passo 4
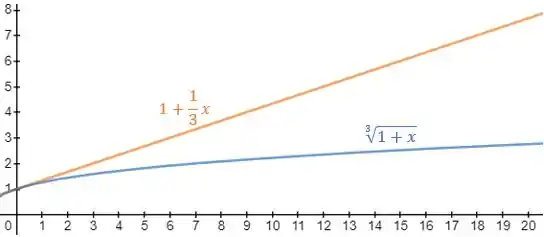
Essa desigualdade ainda pode ser confirmada através do esboço das curvas das funções usadas na inequação. Então, para o nosso caso foi usado o Software online chamados Desmos , no qual foi obtido:
Resposta
