Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.6 - Ex. 15
Se f for uma função injetora tal que , quanto é ?
Passo 1
E aí meus lindos!?
Aqui estamos falando de função injetora, então a gente tem que lembrar o quer é isso ne. Você se lembra?
Uma função é injetora quando cada tem um diferente. Ou seja, dois pontos diferentes tem sempre imagens diferentes .
Agorta temos que notar que estamos lidando com uma função inversa. Na função inversa, o domínio de f se torna o contradomínio e o contradomínio se torna o domínio. Repare nesse esquema:
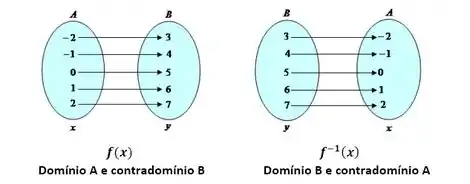
Esses diagramas acima mostram a inversa de uma função injetora. Cada tem apenas um único . E cada tem apenas um único .
Agora vamos aplicar todos esses conceitos na nossa função e vamos achar o valor de:
Passo 2
Sabemos que , então no gráfico da função f, existe o ponto .
Como vimos no passo 1, na função inversa, o domínio de se torna o contradomínio e o contradomínio se torna o domínio. Então na função , a gente inverte os valores acima:
E temos o ponto .
E como a função é injetora, vamos ter apenas um valor de associado a
Portanto