- Se , Mostre que não existe
- Se encontre
- Mostre que tem uma reta tangente vertical em (0,0)
- Ilustre a parte (c) fazendo o gráfico de
Passo 1
Animados pra mais uma questãozinha? Vamos com calma, vai ser de boa!
Temos uma função:
No item a, queremos mostrar que , a derivada de em não existe. Então pra calcular a derivada de , vamos pegar a definição de derivada:
No item b, vamos usar esse mesmo conceito pra calcular a derivada de , nos pontos diferentes de zero. Pra isso, vamos fazer uma série de manipulações da equação de forma que o resultado não seja uma indeterminação.
E no item c vamos usar o resultado anterior pra mostrar que a tangente em 0 é vertical.
Passo 2
Pela definição da derivada:
Nossa função é
Então precisamos primeiro calcular e, pra isso, vamos substituir por em :
Substituindo na definição da derivada:
Como
Arrumando:
Quando a gente aproxima de zero, a gente vai ficar com um número infinitesimalmente pequeno no denominador, então isso significa que cresce indefinitivamente, logo não existe!
Passo 3
Agora vamos para a letra (b), aqui a gente quer calcular com !!
Já começamos a calcular no passo 2:
Mas a gente vai precisar dar uma arrumadinha nisso?! No numerador ambos são elevados a , então...
Aháaa, já da pra ter uma luz!! Vê se o que a gente tem no numerador não parece com aquele caso geral:
Logo, podemos fazer:
Agora a gente vai brincar com o denominador!! Fatorando , temos:
Substituindo, temos:
aparece em cima e em baixo, podemos cortar!
Agora sim, podemos substituir por :
Calculando:
Por fim:
Passo 4
Na letra (c) a gente tem que mostrar que tem uma reta tangente vertical em (0,0), então bora lá!
Lá no passo 2, a gente encontrou que:
Matematicamente dizemos que esse limite é infinito, porque dividindo 1 por um número infinitesimalmente próximo de zero, dá um número muito muito muito grande (infinito).
Mas a derivada é a inclinação da reta tangente. E ter uma inclinação infinita, nesse caso, significa que a reta está completamente na vertical.
Passo 5
Fazendo o gráfico da função, temos
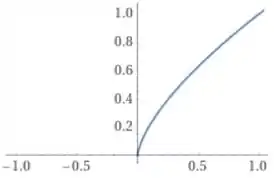
Repara que no ponto de interesse, a tangente é vertical, ou seja, tem inclinação infinita!
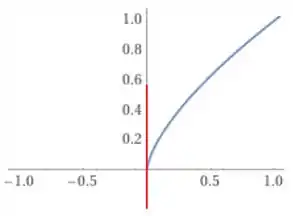
Resposta
(b)
(c) tem uma tangente vertical em