Uma força eletromotriz de 60 V é aplicada a um circuito elétrico simples consistindo de um resistor de 20 ohms e de um indutor, agora uma função do tempo , descrito como L= 0,04 + 0,01t. com t variando entre [0,500] . Se i amperes for a corrente de t s e i =0 quanto t=0. A) Expresse i como função de t. B) ache a corrente teoricamente máxima
Passo 1
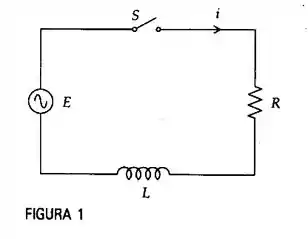
A figura 1 mostra um exemplo de circuito RL. Se a gente usar a Lei das malhas Podemos dizer que :
Então já temos uma boa expressão para achar i. A gora so falta usar os dados de contorno do sistema .
Passo 2
- Expresse i como função de t.
- ache a corrente teoricamente máxima
E sabemos que
E = 60 V
L= 0,04 + 0,01t.
R = 20
I = 0, se t =0
Assim vamos plotar nossos valores na função.
Vamos resolver essa equação por separação de variáveis.
Pronto, agora basta integrar nos dois lados.
Agora é a parte do pulo do gato. Vamos usar : quando t = 0, i = 0
Agora que já temos C, vamos isolar a corrente pra deixar ela evidente
Podemos Melhorar a cara dessa função:
Assim i em função de t fica
Passo 3
Lembra de maximização de funções? Quando queremos uma função seja máxima precisamos derivar e igualar a zero.
Podemos simplificar essa função como
Como sabemos, uma função com a forma só se anula com x tendendo a infinito. Contudo nossa função é limitada no intervalo [0,500]
Então temos t +4 = 0
t = -4 s
Tempos negativos estão fora do nosso intervalo
Eita! Maximizar nossa função não ajudou em nada. Não nos trouxe nenhum resultado especifico. Como prosseguir?
Não podemos esquecer do Teorema de Weierstrass. Num intervalo fechado [a,b], obrigatoriamente minha função vai ter um máximo e um mínimo.
E Além disso os candidatos a Máximos e mínimos são os pontos que anulam a derivada de f e os extremos do nosso intervalo. Temos então que testar t = 0 e t = 500.
Em T = 0s
Em t = 500s
Uma dica : Em física fazemos uma distinção entre infinito e muito , muito grande.
Se pegarmos podemos dizer que é equivalente a
Olhando para a exponencial, podemos escrever , onde
Essa expressão vai explodir para o infinito quando for muito maior em relação a 40.
E de fato, nosso caso é esse. Então podemos Assumir que é muito , muito próximo de zero. (Se formos jogar numa calculadora, esse termo esta na ordem de , ou seja, realmente muito próximo de zero. )
Então i = 3A
Resposta
A )