Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.6 - Ex. 3

Para a força variável F ( x ) do Exercício 2, considere a distância d para qual o trabalho realizado pela força sobre a partícula quando esta se move de x = 0   até x = d é a metade do trabalho realizado quando a partícula se move de x = 0 e x = 5 . Examinando o gráfico de F , decida se d é maior ou menor do que 2,5 . Explique seu raciocínio e, então, obtenha o valor exato de d .

Passo 1

Ele quer saber se d é maior ou menor do que 2,5 e qual é o valor exato de d .

Ele diz que d é quando o trabalho é a metade do que foi calculado no exercício 2, assim:

W d = 140 2 = 70   N . m

Passo 2

O trabalho é dado por:

W = ∫ a b F x d x = á r e a   e m b a i x o   d a   c u r v a

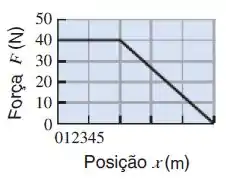
A gente vê pelo gráfico, que no primeiro momento a nossa força é constante, e nesse período, o trabalho vale:

W 1 = 40 ⋅ 2 = 80   N . m

Ih, repara que isso já é maior que W d , e esse valor já acontece em x = 2   m . Logo, certamente d é menor que 2,5 , porque provamos que ele é menor que 2 .

Passo 3

E qual é o valor de d ? Como nesse intervalo, F ( x ) é constante e igual a 40   N , podemos usar a fórmula:

W d = d ⋅ F ∴ 70 = d ⋅ 40

Isolando o d :

d = 1,75   m

Resposta

d = 1,75   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1) Sobre uma partícula que se desloca sobre o eixo x atua uma força cuja componente na direção do deslocamento é f x . Calcule o trabalho realizado pela força quando a partícula se desloca de x=a até
9) De acordo com a lei da gravitação de Newton, a Terra (massa M ) atrai uma partícula de massa m com uma força de intensidade ( G é a constante gravitacional) f r = G M m r 2 Onde r é a distância da
13) A B de constate k está presa ao suporte A e a um corpo de massa m . O comprimento normal da mola é l . Desprezando o atrito entre o corpo B e a barra horizontal, mostre que a aceleração a do corpo
Sobre uma partícula que se desloca sobre o eixo Ox atua uma força F → de intensidade 3N e que forma com o eixo Ox um ângulo x radianos.Calcule o trabalho realizado por F → quando a partícula se desloc
3) Uma partícula de massa m=1 desloca-se sobre o eixo O x sob a ação da força resultante F → x =- xi → . Sabe-se que no instante t = 0 a partícula encontra-se na posição x = 1ev = 2 . Verifique que, p