Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.10 - Ex. 42

A forma de um estacionamento é irregular e o comprimento do terredo de oeste a leste é 240   m . No extremo oeste do terreno a largura é de 150   m e no extremo leste é de 175   m . Em 40,80,120,160 e 200   m do extremo oeste, as larguras são 154 ,   158 ,   165 ,   163 e 172   m , respectivamente. Use a regra de Simpson para aproximar a área do estacionamento.

Passo 1

Vamos lá, meio confusa essa questão, mas basicamente a parada é essa aqui. Ele tem um estacionamento, com uma parede meio irregular, eu fiz um esboço de um gráfico com essas parada, olha só:

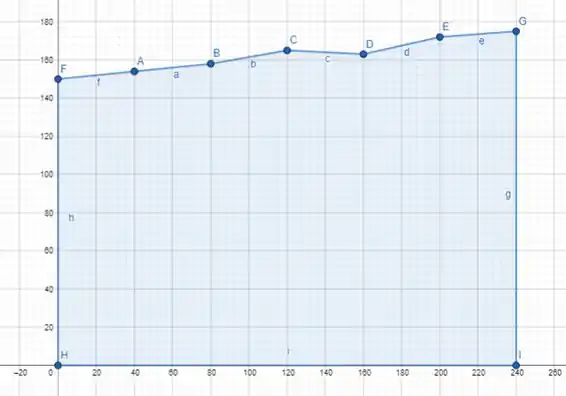
Seria algo mais ou menos assim.

Ele quer a área disso, se chamarmos aquela curva que passa pelos pontos F , A , B , C , D , E , G DE f x , podemos fazer a integral de 0 até 240 para achar a área:

A = ∫ 0 240 f x d x

Mas não fazemos ideia da expressão da f x .

Aí, vamos usar a regra de Simpson.

Passo 2

A regra de Simpson é:

∫ a b f x d x = b - a 3 n f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + … + 2 f x n - 2 + 4 f x n - 1 + f x n

Aquele n é a quantidade de intervalos que vamos ter. Reapra que temos 6 intervalos entre os pontos que ele deu.

Então, devemos fazer:

n = 6

E fazendo

b = 240

a = 0

Vamos ter:

∫ 0 240 f x d x = 240 18 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + f x 6

∫ 0 240 f x d x = 40 3 f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + 2 f x 4 + 4 f x 5 + f x 6

Aquele x i todos, são exatamente os pontos que ele deu. Então temos:

x 0 = 0 → f x 0 = 150

x 1 = 40 → f x 1 = 154

x 2 = 80 → f x 2 = 158

x 3 = 120 → f x 3 = 165

x 4 = 160 → f x 4 = 163

x 5 = 200 → f x 5 = 172

x 6 = 240 → f x 6 = 175

Passo 3

Pegando esses valores que achamos, vamos jogar na fórmula:

A = ∫ 0 240 f x d x = 40 3 150 + 4 ∙ 154 + 2 ∙ 158 + 4 ∙ 165 + 2 ∙ 163 + 4 ∙ 172 + 175

A = ∫ 0 240 f x d x = 40 3 2931 = 39080   m 2

Resposta

A = 39080   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o valor exato da integral a seguir é π , interpretando-a como medida da área de uma região. Aproxime-se dess resultado usando a regra do trapézio para valor de n dado, com três casas decima
Mostre que o valor exato da integral abaixo é igual a π , interpretando como medida da área de uma região. Use a regra de simpsom para n=6 e prove por aproximação que o valor da integral é π . ∫ 0 1 4
96. Se n for um número inteiro positivo, prove que ∫ 0 π s e n 2 n xd x = 1 2 π .
Nos exercícios 97 e 98, ache um valor aproximado para a integral, usando a regra do trapézio com n = 4 . Expresse o resultado com até três casas decimais.98. ∫ 1 9 5 1 + x 3
Nos exercícios 97 e 98, ache um valor aproximado para a integral, usando a regra do trapézio com n = 4 . Expresse o resultado com até três casas decimais.97. ∫ 0 2 1 + x 2d x