Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.4 - Ex. 25
A fórmula
deduzida do Exercício 5, expressa a curvatura de uma curva plana duas vezes diferenciável como uma função de . Encontre a função de curvatura de cada uma das curvas nos Exercícios 23-26. Em seguida, desenhe com sobre o intervalo dado. Você encontrará algumas surpresas.
25.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No problema dado, temos que
Diferenciando os termos,
Ok, vamos usar a derivada novamente
Passo 2
Substituindo as expressões para e na fórmula
Trocando os termos já conhecidos
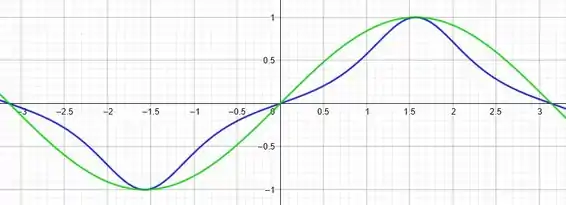
No gráfico temos a seguinte configuração
Resposta
Exercícios de Livros Relacionados
Mostre que a curvatura de uma curva plana descrita por σ t = x t , y t é k t = x ' t y ' ' t - y ' t x ' ' ( t ) x ' t 2 + y ' t 2 3 2 Observe que esta equação se reduz à equação (1.13) quando a curva
A fórmula κ x = f ' ' ( x ) 1 + f ' x 2 3 / 2 deduzida do Exercício 5, expressa a curvatura κ ( x ) de uma curva plana duas vezes diferenciável y = f ( x ) como uma função de x . Encontre a função de
A fórmula κ x = f ' ' ( x ) 1 + f ' x 2 3 / 2 deduzida do Exercício 5, expressa a curvatura κ ( x ) de uma curva plana duas vezes diferenciável y = f ( x ) como uma função de x . Encontre a função de
A fórmula κ x = f ' ' ( x ) 1 + f ' x 2 3 / 2 deduzida do Exercício 5, expressa a curvatura κ ( x ) de uma curva plana duas vezes diferenciável y = f ( x ) como uma função de x . Encontre a função de