Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 47
- Identifique os valores extremos locais das funções nos domínios dados informe onde eles ocorrem
- Qual dos valores extremos, se houver, é absoluto
- Fundamente suas conclusões como uma calculadora ou programa gráfico
Passo 1
a)
Primeiramente, necessitamos calcular a derivada de fpara encontrar os pontos críticos
Igualamos a zero
Ponto crítico:
Passo 2
Agora, vamos fazer o estudo do sinal para verificar onde a função cresce e decresce. Beleza?
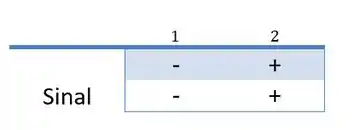
Logo,
e
Portanto, temos:
Máximo local é 1 quando
Mínimo local é 0 quando
b) Nesse caso, não temos o máximo absoluto e o mínimo absoluto é 0 quando .
Passo 3
- Segue o gráfico, feito no geogebra
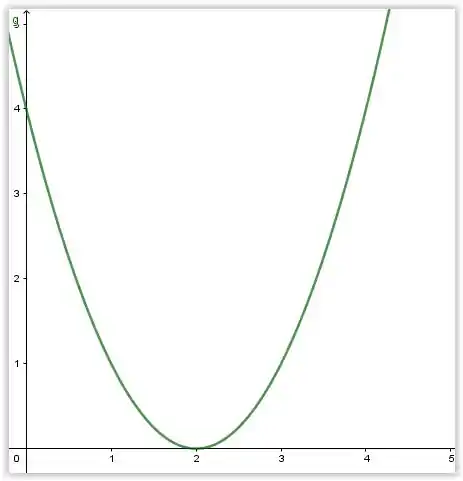
Resposta
- Máximo local é 1 quando ;mínimo local é 0 quando
b) Nesse caso, não temos o máximo absoluto e o mínimo absoluto é 0 quando .
Exercícios de Livros Relacionados
Encontre os números críticos da função. g t = 5 t 2 3 + t 5 3
Encontre os números críticos da função. g x = | 2 x + 3 |
Encontre os valores máximo e mínimo locais e absolutos de f . f θ = sin θ- 2 π ≤ θ ≤ 2 π
Use o gráfico para estabelecer os valores de máximo e mínimo locais e absolutos da função.
Encontre os números críticos da função. f x = x ln x