Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 88
Mostre que se , então , mas não é uma ponto de inflexão do gráfico de .
Passo 1
Oieee, bora resolver essa juntinhoi??
Para mostrar que , então , mas não é um ponto de inflexão do gráfico de podemos utilizar a definição de ponto de inflexão e a segunda derivada.
Primeiro, vamos calcular as derivadas de
Agora, vamos calcular
Portanto, de fato,
Passo 2
Agora, para verificar se é um ponto de inflexão, vamos analisar a mudança de concavidade ao redor deste ponto.
Um ponto de inflex��o ocorre quando a concavidade de uma função muda.
Isso acontece quando a segunda derivada troca de sinal.
Como não podemos usar essa condição para determinar se é um ponto de inflexão.
Em vez disso, precisamos analisar a concavidade antes e depois de
Passo 3
Vamos analisar a concavidade da função em torno de
Se , então o que significa que a função é côncava para cima.
Se então novamente, ou seja, também é côncava para cima.
Isso significa que a função é côncava para cima em ambos os lados de o que implica que não há mudança de concavidade.
Portanto, não é um ponto de inflexão do gráfico de
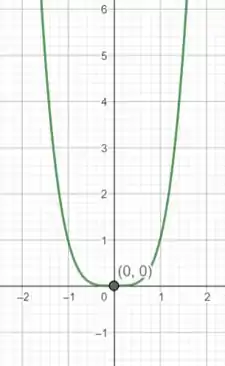
Resposta
Vide a explicação.