Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 42

42. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.

y = x 2 + 1 2 x 2 - 3 x - 2

Passo 1

Opa, vamos fazer essa questão! Temos a seguinte curva:

y = x 2 + 1 2 x 2 - 3 x - 2

E o enunciado pede pra a gente encontrar as suas as assíntotas horizontais e verticais e depois confirmar que o cálculo está certo esboçando o gráfico da função!

Para acharmos as assíntotas horizontais, vamos analisar os limites para x tendendo a ∞ e - ∞ Já as assíntotas verticais geralmente estão relacionados a um ponto onde a nossa função não esta definida.

Bora colocar a mão na massa então!

Passo 2

Começando pelas assíntotas horizontais, vamos analisar os limites para ∞ e - ∞ .

lim x → ∞ ⁡ x 2 + 1 2 x 2 - 3 x - 2

Concorda comigo que: ∞ 2 ≫ 1

2 ∞ 2 ≫ 3 ∞

2 ∞ 2 ≫ 2

Então vamos reescrever o nosso limite assim:

lim x → ∞ ⁡ x 2 + 1 2 x 2 - 3 x - 2 = lim x → ∞ ⁡ x 2 2 x 2 = lim x → ∞ ⁡ 1 2

lim x → ∞ ⁡ 1 2 = 1 2

Da mesma forma temos que:

lim x → - ∞ ⁡ 1 2 = 1 2

Então isso nos diz que temos uma assíntota horizontal em 1 2 . Portanto, y = 1 2 é uma assíntota horizontal!

Passo 3

Lá em cima falamos que assíntotas verticais estão relacionados a um ponto onde a nossa função não está definida, vamos observar a nossa função:

y = x 2 + 1 2 x 2 - 3 x - 2

A medida que aproximamos o nosso denominador a 0 nosso y tende a ∞ , isso porque estamos fazendo uma divisão por um número beeem pequeninho, e o que acontece nesse caso?!

Isso mesmo, temos um resultado beeeem grande, que pode ser positivo ou negativo! Então vamos calcular as raízes do polinômio do denominador:

2 x 2 - 3 x - 2 = 0

x = - b ± b 2 - 4 a c 2 a

x = 3 ± 3 2 - 4 2 - 2 2 2

x = 2

x = - 0,5

Dessa forma teremos assíntotas verticais em x = 2 e x = - 0,5 .

Passo 4

Fazendo um gráfico, temos:

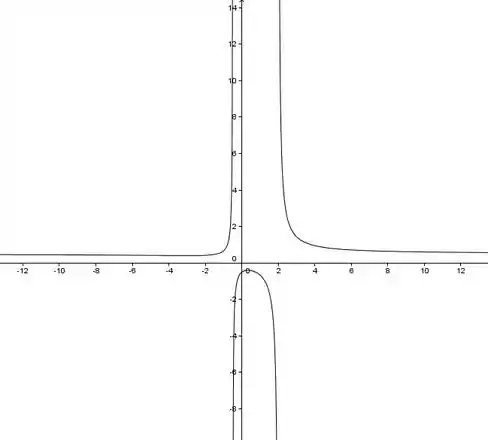
Pelo gráfico, podemos confirmar que as assíntotas são realmente aquelas.

Resposta

Assíntota horizontal:

y = 1 / 2

Assíntota vertical:

x = 2 e x = - 1 / 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 2 x + 1 x - 2
45. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = x 3 - x x 2 - 6 x + 5
36. Encontre o limite ou demonstre que não existe. lim x → ∞⁡ s e n 2 ( x ) x 2 + 1
Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 1 + x 4 x 2 - x 4
32. Encontre o limite ou demonstre que não existe. lim x → - ∞ ⁡ 1 + x 6 x 4 + 1