Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 5

Para a função f , cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, explique por quê .

(a) lim x → 1 ⁡ f x (b) lim x → 3 - ⁡ f x (c) lim x → 3 + ⁡ f x

(d) lim x → 3   ⁡ f x (e) f ( 3 )

Passo 1

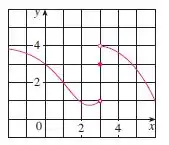
Falaee, belezinha??? Bom... a questão nos deu o seguinte gráfico:

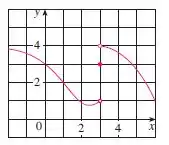
E, com esse gráfico, quer que calculemos as seguintes expressões:

(a) lim x → 1 ⁡ f x (b) lim x → 3 - ⁡ f x (c) lim x → 3 + ⁡ f x

(d) lim x → 3   ⁡ f x (e) f ( 3 )

Para isso, devemos analisar para onde o x está tendendo em cada limite e comparar com o gráfico da função.

E aí?? Bora lá?? 😉

Passo 2

  1. Quando x → 1 , analisando o gráfico começando tanto pela esquerda quanto pela direita temos que f x   a p r o x i m a   d e   2 , logo pela definição:

    2. lim x → a ⁡ f x = L         s e   e   s o m e n t e   s e       lim x → a - ⁡ f x = L         e       lim x → a + ⁡ f x = L

    Temos que:

    lim x → 1 ⁡ f x = 2

    Passo 3

  2. Como x → 3 - , devemos começar a analisar o gráfico pela esquerda.

    3. Assim analisando desse modo quando x = 3 , f x aproxima de 1, logo lim x → 3 - ⁡ f x = 1 .

    Passo 4

  3. Como x → 3 + , devemos começar a analisar o gráfico pela direta.

    4. Assim analisando desse modo quando x = 3   , f x   a p r o x i m a   d e   4 , logo lim x → 3 + ⁡ f x = 4 .

    Passo 5

  4. Para x → 3 , devemos considerar os limites pela esquerda e pela direita. Por definição temos que:

    5. lim x → a ⁡ f x = L         s e   e   s o m e n t e   s e       lim x → a - ⁡ f x = L         e       lim x → a + ⁡ f x = L

    Logo como os limites laterais ( pela esquerda e pela direita) são diferentes , concluímos que lim x → 3 ⁡ f x não existe.

    Passo 6

  5. Para f ( 3 ) , devemos observar no gráfico para qual valor de f ( x ) com x = 3 pertence a imagem do gráfico. Assim, temos que f 3 = 3 .

Outra maneira de saber em gráficos descontínuos como este é verificar para aquele ponto de descontinuidade, neste caso em x = 3 ,qual ponto tem uma “bolinha fechada”, isso indica que pertence a imagem.

Resposta

  1. lim x → 1 ⁡ f x = 2
  2. lim x → 3 - ⁡ f x = 1
  3. lim x → 3 + ⁡ f x = 4
  4. lim x → 3 ⁡ f x não existe.
  5. f 3 = 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = x 3 ⋅ x + 2 2 ⋅ ( x - 1 )
Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = x 2 ⋅ x 2 - 1 2 ⋅ ( x + 2 )
Seremos capazes de mostrar, no Capítulo 9 do Volume II, que, sob certas condições, a velocidade v ( t ) de uma gota de chuva caindo no instantet é v t = v * ( 1 - e - g t v * ) Encontre lim t → ∞ ⁡ v
Encontre os limites quando x → ± ∞ . Use essa informação, bem como as interseções com os eixos, para fazer um esboço do gráfico. y = 3 - x ⋅ 1 + x 2 ⋅ 1 - x 4
Faça um esboço da curva y = x n( ni n t e i r o ) nos seguintes casos. n = 0 n0( ní m p a r ) í n0( np a r ) n0( ní m p a r ) í n0( np a r ) Então use esses esboços para calcular os seguintes limites