Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.2 - Ex. 4
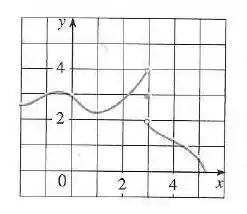
Para a função cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê.
Passo 1
Olá, meu nobre amigo. Vamos começar mais uma resolução !
Veja bem, queremos aqui encontrarmos os limites da função em diferentes pontos, mas para isso iremos utilizar o gráfico.
Como fazer isso? E quais pontos você deve prestar mais atenção? Vem comigo que te conto.
Primeira coisa, ou uma das primeiras coisas que você deve notar ao procurar o limite utilizando o gráfico é em casos de limite
Você deve encontrar os limites laterais , isso é, quando nos aproximamos de por valores infinitesimalmente menores que , represetando isso por , nós iremos chegar ao valor pela esquerda.
Agora quando estivermos nos aproximando de por valores infinitesimalmente maiores que , represetando isso por , nós iremos chegar ao valor pela direita. Caso os valores que encontrarmos nessas duas situações forem iguais, temo que o limite , existe, caso eles sejam diferentes o limite não existe.
Outro ponto a se prestar atenção é quando formos calcular , devemos prestar atenção na bolinha nos gráficos. Uma bolinha fechada indica que naquele ponto de a função está definida onde a bolinha indica em . Os pontos de bolinha aberta não estão definidos na função.
Passo 2
- A função é definida de ambos os lados de e, considerando o gráfico desta função, não é difícil concluir que podemos fazer os valores da função infinitesimalmente próximos ao valor , tomando suficientemente próximo a de ambos os lados, mas não igual a . Portanto, pela definição de limite, obtemos que
- A função é definida no lado esquerdo de e, considerando o gráfico desta função, vemos que podemos fazer os valores arbitrariamente próximos ao valor , quando deixamos suficientemente próximo a pelo lado esquerdo, mas não igual a . Portanto, pela definição do limite unilateral, obtemos que
- A função é definida no lado direito de e, considerando o gráfico desta função, não é difícil concluir que podemos fazer os valores arbitrariamente próximos ao valor , tomando suficientemente próximo a pelo lado direito, mas não igual a . Portanto, pela definição do limite unilateral, obtemos que
- Supondo que o limite exista, então, pelo teorema, temos que
- O valor é representado por um ponto cinza na imagem, o circulo fechado que comentamos no passo 1. Uma vez que este ponto tem coordenadas , obtemos que .
Passo 3
O resultado das partes (b) e (c) implica que a igualdade mostrada acima não se mantém, portanto, nossa suposição não está correta. Logo, o limite não existe.
Resposta
- não existe, pois os limites das letras (b) e (c) não são iguais