A função cujo gráfico é dado a seguir é uma solução de uma das seguintes equações diferenciais. Decida qual é a equação correta e justifique sua resposta.
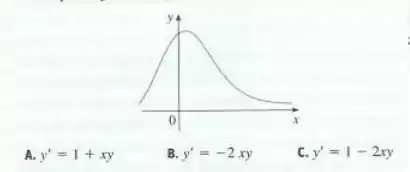
Passo 1
Precisamos analisar as equações dos itens A,B e C, e seus gráficos para ver qual delas respeita o comportamento do gráfico dado.
Passo 2
A. Na primeira equação, ao olharmos pontos pertencentes ao primeiro quadrante (onde ) sabemos que , ou seja, é uma reta com inclinação positiva. Mas note que no gráfico podemos ver que a função decresce em alguns pontos do primeiro quadrante, então , o que não condiz com a nossa conta. Por esse motivo, a primeira equação não pode ser a resposta correta.
Passo 3
B. Vamos analisar a equação , note que quando , , mas podemos ver no gráfico que quando , , portanto essa não pode ser a solução
Passo 4
C. Agora vamos olhar para a equação . Quando , pode ser igual a . Quando , é menor que , o que pode ser verdade pelo gráfico.
Isolando na equação, ficamos com , disso podemos concluir que quando assume valores bem grandes, fica cada vez menor, se aproximando de , como mostra o gráfico.
Com isso, podemos concluir que a equação C é a correta.
Resposta
C.