Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 32
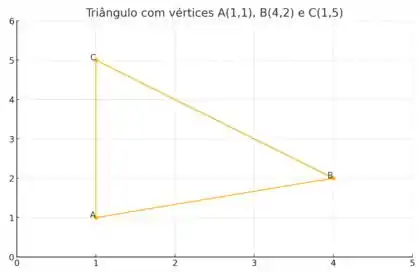
Usando uma ferramenta gráfica e o resultado do Exercício 31, desenhe o trângulo com vértices .
Passo 1
Olá galerinha. Tudo bem?
Vamos resolver essa questãozinha!
A questão quer a construção do gráfico, mas cita também a questão de número que por sinal fala sobre equações paramétricas. Logo teremos que encontrar as equações paramétricas das aresta do triângulo com vértice , e . Ou seja, vamos descobrir a reta que liga os pontos.
Mas como vamos fazer isso?
Vamos lembrar que a forma geral de uma equação paramétrica para um segmento de reta entre dois pontos e é dada por:
Onde é um parâmetro que varia de a . Quando , a operação dá o ponto inicial e quando , a equação dá o ponto final .
Agora é só resolver o segmento , e .
Passo 2
Vamos precisar plotar esse triângulo usando segmentos de retas que unem esses três pontos, dois a dois, a partir da equação paramétrica do segmento de reta que demonstramos na questão anterior.
Para não precisar voltar lá, vou repetir ele aqui:
Assim, vamos definir os segmentos de reta que unem cada um desses pontos.
Passo 3
Começando por :
Ponto e
Substituindo nas equações, temos:
Ou seja,
Onde
Passo 4
Agora vamos para o segmento :
Ponto e
Substituindo nas equações, temos:
Ou seja,
Sendo assim,
Onde
Passo 5
Finalmente, segmento :
Ponto e
Substituindo nas equações, temos:
Ou seja,
Onde
Passo 6
Agora plotando todos esses segmentos:
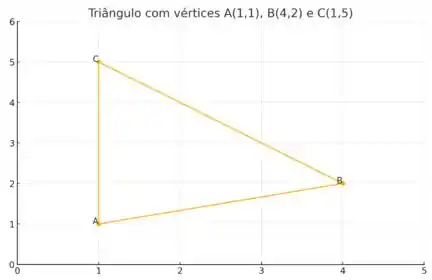
Resposta
