Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 2
Para a função cujo gráfico está na figura abaixo, arranje os números , , , e em ordem crescente.
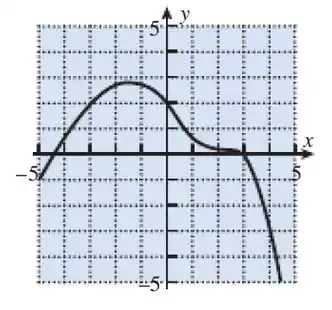
Passo 1
Vamos analisar as retas tangentes nos pontos:
Em temos o único ponto que a reta tangente é crescente, assim sua derivada é maior que zero:
Passo 2
Em , e as retas tangentes são decrescentes.
Sendo que é mais decrescente que os outros pontos, ou seja, a derivada nesse ponto é mais negativa.
E em o menos decrescente, tendo a derivada menos negativa, assim podemos arranjar os números em ordem crescente:
Resposta
Exercícios de Livros Relacionados
Prove que D x n ln x = - 1 n - 1 n - 1 ! x n Sugestão: Use indução matemática.
Use os resultados dos exercícios 65 e 66 para provar que lim x → 1 x b - 1 x - 1 = b Sugestão: Escreva x b - 1 x - 1 = e b ln x - 1 b ln x b ln x x - 1 Então tome s = b ln x e t = x - 1
Prove, usando a definição de uma derivada, que lim x → 0 e a x - 1 x = a
Prove, sem usar a definição de uma derivada, que lim x → 0 a x - 1 x = ln a Sugestão: seja y = a x - 1 e expresse a x - 1 x como função de y , digamos, g y . Então mostre que y → 0 quando x → 0 e
Se o domínio de f for o conjunto de todos os números reais e f ' x = c f x para todo x onde c é uma constante, prove que existe uma constante k para a qual f x = k e c x para todo x .Sugestão: conside