Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 9
Uma função custo é dada.
- Encontre as funções custo médio e custo marginal.
- Use os gráficos das funções na parte (a) para estimar o nível de produção que minimize o custo médio.
- Use o cálculo para encontrar o custo médio mínimo.
- Encontre o valor mínimo do custo marginal.
Passo 1
A ei meu amigo! Vamos resolver mais essa questão?
Ok, temos uma equação de custo e várias coisas para calcular:
Para o item (a), precisamos encontrar o custo médio e o custo marginal. O custo médio é simplesmente o custo total dividido pelo número de unidades produzidas, então dividimos a função do custo total por (número de unidades).
O custo marginal é a derivada do custo total , que nos mostra como o custo muda à medida que aumentamos a produção. Derivada é a palavra-chave aqui.
No item (b), vamos fazer os gráficos de e .
Para o item (c), observamos onde as duas funções se cruzam. Nesse ponto, teremos o mínimo.
Finalmente, no item (d), igualamos a derivada a zero para encontrar o valor mínimo do custo marginal.
O enunciado nos deu essa função:
E é com ela que vamos aplicar nossos conceitos!
Bora lá!
Passo 2
(a) A função custo médio é encontrada dividindo o custo total pelo número de unidades. Então:
A
função custo marginal é a derivada do custo total:
Usando a regra da potência para as derivadas, temos:
Aplicando na nossa função:
Passo 3
(b) Usando uma calculadora gráfica, vamos representar o gráfico de e :
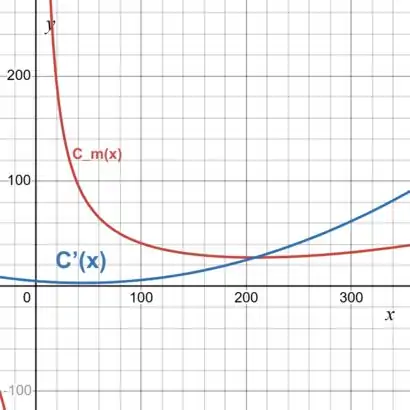
A condição para que o custo médio seja mínimo é que ele seja igual ao custo marginal:
Olhando os gráficos, vemos que isso ocorre entre .
Passo 4
(c) Agora usamos a expressão de para encontrar seu valor mínimo, que ocorre em ou em :
Olhando para os valores, vemos que:
Passo 5
(d) Agora calculamos o custo marginal mínimo. Podemos fazer isso olhando o gráfico ou derivando e igualando a zero. Vamos fazer pela derivada.
Igualando a zero:
Olhando para o gráfico de , verificamos que temos para esse valor de de fato um mínimo. Então calculamos esse mínimo:
Resposta
(a)
(b)
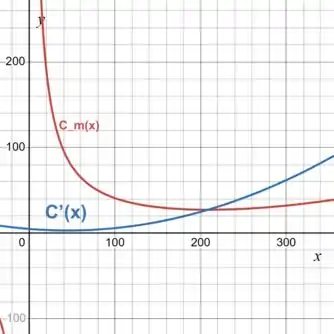
(c)
(d)