Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 10
Uma função custo é dada.
Encontre as funções custo médio e custo marginal.
Use os gráficos das funções na parte (a) para estimar o nível de produção que minimize o custo médio.
Use o cálculo para encontrar o custo médio mínimo.
Encontre o valor mínimo do custo marginal.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função custo de uma produção
E nosso objetivo é obter e plotar os gráficos das funções custo medio e custo marginal. A partir dos seus gráficos, o problema pede para que a gente estime um nível de produção que minimize o custo médio.
Parece complicado?
A principio, para obter a função custo médio temos que lembrar que o custo médio de algo é dado pelo custo total sobre o número, no caso, de produção. Ou seja
Já o custo marginal é dado pela taxa de variação do custo... podemos interpretar isso como a derivada do custo total .
E para estimar o nível de produção que minimize o custo médio temos que observar no gráfico o ponto onde . Aí, substituímos esse ponto no custo médio para calcular o custo médio mínimo.
Para encontrar o valor mínimo do custo marginal vamos usar o que aprendemos nos pontos extremos de uma função... derivamos e igualamos a .
Sacou? Bora começar!
Passo 2
Como vimos no passo 1, a função custo médio é encontrada dividindo o custo total pelo número de unidades.
Então:
Já a função custo marginal é a derivada do custo total:
Pela regra da potência...
Tranquilo até aqui?
Passo 3
Agora temos que plotar os gráficos de e ...
Usando uma calculadora gráfica, vamos representar o gráfico de e :
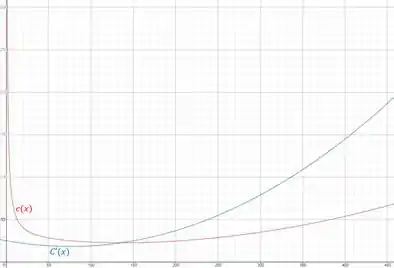
A condição para que o custo m��dio seja mínimo é que ele seja igual ao custo marginal:
Olhando os gráficos, vemos que isso ocorre para .
Show?
Passo 4
Agora usamos a expressão de para encontrar seu valor mínimo, que ocorre em como vimos no passo anterior:
Então:
Bacana, não é?
Passo 5
Agora calculamos o custo marginal mínimo.
Podemos fazer isso olhando o gráfico ou derivando e igualando a zero. Vamos fazer pela derivada aplicando a regra da potencia novamente.
Igualando a zero:
Olhando para o gráfico de , verificamos que temos para esse valor de de fato um mínimo. Então calculamos esse mínimo:
E fim! O que achou? Responde Aí!
Resposta
(a)
(b)
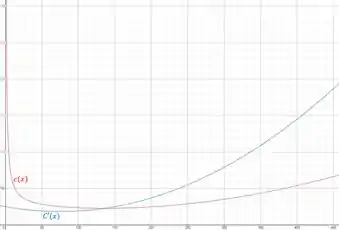
(c)
(d)