Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 11
Uma função é dada por uma fórmula. Determine se é injetora.
Passo 1
Bom, pessoal, para saber se uma função é injetora, vamos ver o conceito de função de injetora.
Uma função injetora é uma função que para cada valor no contradomínio existe apenas um valor no domínio associado. Em outras palavras, cada , vai ter apenas um único .
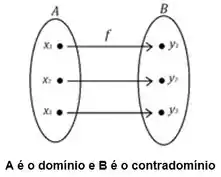
Um jeito de saber se uma função é injetora é usar o teste da reta horizontal. Se a gente pode traçar qualquer reta horizontal e ela cruzar a curva em mais do que 1 ponto, então a função não é injetora.
Passo 2
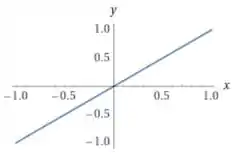
Agora vamos ver a fórmula da questão. Primeiro vamos relembrar o gráfico da função
Que é uma reta de inclinação 1 e que passa pela origem:
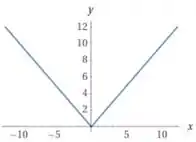
Nossa função é o módulo de :
E o módulo faz tudo ficar positivo lembra? Se o valor é positivo, nada muda. Mas se é negativo, fica positivo:
Então, se tudo que é negativo fica positivo, é como refletir a parte que tá embaixo do eixo pra cima:
Passo 3
Vamos pegara reta
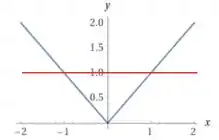
É fácil ver que a função passa por essa reta em dois pontos:
Ou seja, temos um valor de que tem mais de um associado (tem outros vários, mas 1 já basta). O valor está associado a e .
Então a função não é injetora!
Resposta
A função não é injetora.