Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 12
Uma função g é dada por uma fórmula. Determine se g é injetora.
Passo 1
Olá, meu querido aluno. Vou te ajudar a resolver essa atividade hoje.
A gente tem uma função:
E a gente quer determinar se essa função é injetora. Para isso, precisamos primeiro saber o que são funções injetoras.
Uma função injetora, também conhecida como uma função unária ou função injetiva, é uma função matemática que atribui um único elemento do conjunto de domínio a cada elemento do conjunto de imagem. Em outras palavras, uma função é injetora se cada elemento no domínio é mapeado para um único elemento no contradomínio. Isso significa que diferentes elementos do domínio não podem ser mapeados para o mesmo elemento no contradomínio.
Veja abaixo um exemplo de uma função injetora, onde é conjunto do domínio, e é conjunto do contradomínio.
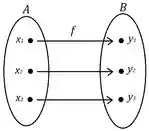
Uma maneira de testar se uma função é injetora é usar o teste da linha vertical. Se uma linha vertical corta o gráfico da função em mais de um ponto, então a função não é injetora. Se nenhuma linha vertical corta o gráfico da função mais de uma vez, então a função é injetora.
Passo 2
Vamos então plotar o gráfico dessa função com o auxílio do GeoGebra:
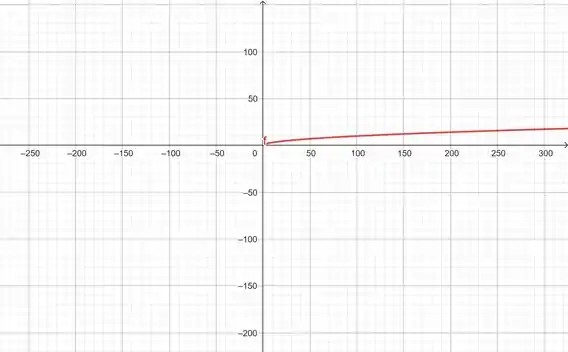
Aqui, sabemos que dois valores de nunca vão possuir a mesma raiz quadrada. Sempre um valor de estará associado a apenas um valor de . Assim, a função é injetora.
E também podemos ver pelo gráfico que ser traçarmos linhas verticais por todo o gráfico ela só irá tocar em um ponto de cada vez.
Resposta
A função g é injetora.