Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.8 - Ex. 33
33.
A função definida por
é denominada função de Bessel de ordem .
(a) Encontre seu domínio.
(b) Trace as primeiras somas parciais na mesma tela.
(c) Se seu SCA tiver funções de Bessel programadas, trace na mesma tela das somas parciais na parte (b) e observe como as somas parciais aproximam de .
Passo 1
E aí pessoal, tudo beleza?
A questão nos deu essa função de Bessel, de ordem :
e três itens pra gente resolver.
No item (a), precisamos saber qual domínio da função;
Em (b) as primeiras somas parciais e;
Em (c) por algum programa resolver criar um gráfico pelas somas parciais descoberta no item anterior.
Calma, passo a passo, vamos lá!
Passo 2
(a) Pra encontrar o domínio dessa função, temos que encontrar pra quais valores de essa série converge. Então bora usar o Teste da Razão?
Lembra que:
Se , a série converge.
Se ou , a série diverge.
Se , é inconclusivo, nada podemos afirmar.
Quem seria nosso ?
Assim, vamos colocar na fórmula do Teste da Razão:
Pela divisão de frações, invertemos o denominador multiplicando:
Organizando um pouco mais...
Como esse limite é sempre , que é menor do que , a série converge pra qualquer , ou seja, o domínio da função de Bessel é .
Passo 3
(b) Agora vamos calcular as primeiras somas parciais para poder traçá-las:
Vamos organizar os fatorias dos denominadores, hein?
Passo 4
(c)
Como queremos ver o gráfico dessas somas, podemos ver que elas convergem em certo ponto:
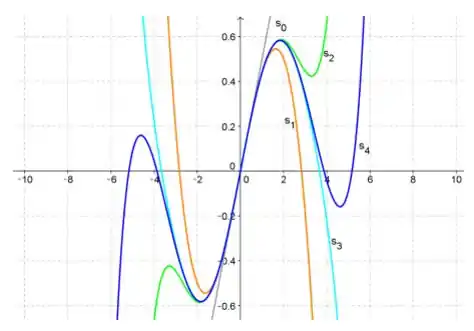
Resposta
(a)