Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.8 - Ex. 34

A função definida por

é denominada função de Airy, em homenagem ao matemático e astrônomo inglês sir George Airy (1801-1892).

(a) Encontre o domínio da função de Airy.

(b) Trace as primeiras somas parciais na mesma tela.

(c) Se seu SCA tiver funções de Airy programadas, trace na mesma tela que as somas parciais na parte (b) e observe como as somas parciais aproximam .

Passo 1

(a) Beleza, galera? Pra encontrar o domínio dessa função, temos que encontrar pra quais valores de essa série converge. Então seria uma ótima ideia usar o Teste da Razão, mas como vamos usá-lo se não sabemos quem é e ?

Pra resolver isso, perceba que os termos da série podem ser definidos recursivamente, olha só:

Não se preocupe, é realmente difícil enxergar essa relação de recorrência, mas pode conferir se quiser!

Passo 2

Show! Agora sim podemos usar o Teste da Razão:

Como esse limite é sempre , que é menor do que , a série converge pra qualquer , ou seja, o domínio da função de Airy é .

Passo 3

(b) Beleza! Vamos traçar algumas somas parciais da série que define a função de Airy:

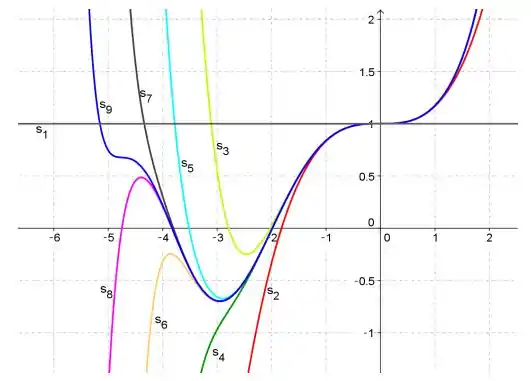
Passo 4

(c)

Resposta

(a)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o raio de convergência e o intervalo de convergência da serie ∑ n = 1 ∞ - 1 n 4 n n x n

35.Uma função f é definida por f x = 1 + 2 x + x 2 + 2 x 3 + x 4 + … isto é, seus coeficientes são c 2 n = 1 e c 2 n + 1 = 2 para todo n ≥ 0 . Ache o intervalo de convergência e encontre uma fórmula e

Mostre que, se l i m n → ∞| c n | n = c onde c ≠ 0 , então o raio de convergência da série de potências ∑ c n x n é R = 1 c .

Suponha que a série ∑ c n x n tenha raio de convergência 2 e que a série ∑ d n x n tenha raio de convergência 3 . O que você pode dizer sobre o raio de convergência da série ∑ ( c n + d n ) x n ? Expl

Suponha que a série de potências ∑ c n x - a n satisfaça c n ≠ 0 para todo n . Mostre que, se l i m n → ∞c n c n + 1 existir, então ele será igual ao raio de convergência da série de potências.