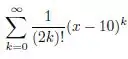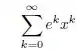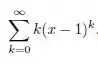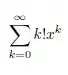Exercícios de Raio e Intervalo de Convergência - Lista de Exercícios Resolvida

Determine para quais valores de a série converge:

Encontre o raio de convergência e o intervalo de convergência da série.

Estude a convergência da série de potências:

Encontre o raio de convergência e o intervalo de convergência da série.

Determinar o raio de convergência da série de potências

Determine o intervalo e o raio de convergência das séries de potência a seguir:

Sabendo que:

Determine o raio de convergência da série de potências:

Determine o intervalo de convergência da série:

Calcule o termo geral da expansão em série de potências de da função abaixo e ache seu intervalo de convergência.

Considere a série de potências

Encontre o raio de convergência e o intervalo de convergência dessa série.

Determine o raio de convergência e o intervalo de convergência da série

Determine o raio de convergência e o intervalo de convergência

Determine o intervalo de convergência

Considere a sequência satisfazendo . Determinar o raio de convergência da série de potências

Determine para quais valores de a série converge:

Obtenha todos os valores reais de para os quais a série abaixo é convergente:

2 – Encontre para quais valores de a série

Converge.

O raio de convergência e o intervalor de convergência da série de potências são respectivamente:

Escolha uma opção:

a. e

b. e

c. e

d. e

e. e

f. e

g. e

h. e

i. e

j. e

k. e

Seja a função definida pela série de potências

1. Ache o domínio de

Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

5)

Verifique se cada uma das afirmações abaixo é verdadeira ou falsa. Justifique provando as verdadeiras e apresentando um contraexemplo para as falsas

tem raio de convergência , então as séries também tem raio de convergência

Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

6)

Encontre o intervalo de convergência da série

Não esqueça de testar os extremos do intervalo, se for o caso.

Determine o raio de convergência da série de potências

4 – Estude detalhadamente o intervalo de convergência da série de potência .

Questão 3: Encontre o raio de convergência e o intervalo de convergência de

Considere a função , definida pela série de potências

a) Determine o raio e o intervalo de convergência dessa série

Considere a função , definida pela série de potências

a) Determine o raio e o intervalo de convergência dessa série

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

Encontre o intervalo de convergência da série

Não esqueça de testar os extremos do intervalo, se for o caso.

Encontre a região de convergência da série de potências:

Após explicitar a série de Taylor de centrada em , determine o raio de convergência.

Dadas as séries

considere as afirmações:

(I) (A) converge para , (B) diverge para .

(II) (A) converge para , (B) diverge para e .

(III) (A) diverge para , (B) diverge para .

(IV) (A) converge para , (B) converge para .

Podemos afirmar que são corretas:

a) Apenas (IV).

b) Apenas (I) e (III).

c) Apenas (II) e (IV).

d) Apenas (III).

e) Todas são falsas.

Seja

Determine os valores de tais que é convergente.

Justifique se as seguintes afirmações são verdadeiras ou falsas

(c) (1.0) O raio de convergência da série de potências satisfaz a equação

Determine o conjunto de valores de para o qual a série , converge.

Determine o raio de convergência e o intervalo de convergência da série

Para cada série de potência abaixo calcular o raio de convergência e o intervalo de convergência:

a)

b)

Determine o intervalo de convergência da série de potências

Determine para quais valores de a série converge:

Questão 3) Consideremos a seguinte série de potências

1. Determinar o raio de convergência e o intervalo de convergência (domínio) de .
2. Determinar o raio de convergência e o intervalo de convergência (domínio) de .

Determinar o raio de convergência da série de potências

Considere a série de potências

1. Determine o raio e o intervalo de convergência da série acima.
2. Para quais valores de a série converge absolutamente? Para quais valores de a série converge condicionalmente?

Questão 2: Considere a série de potências

1. Determine o intervalo de convergência desta série.

Justifique se as seguintes afirmações são verdadeiras ou falsas

(c) (1.0) O raio de convergência da série de potências satisfaz a equação

(2.0) Encontre o raio de convergência e o intervalo de convergência de

Para quais valores de abaixo a série

É convergente

Escolha uma ou mais:

a)

b)

c)

d)

Em relação a uma série

É correto afirmar:

a) se convergir então a série converge.

b) se a série converge, então

c) se a série converge, então .

d) a série converge se, e somente se, .

e) se a série converge, então .

Determine o raio de convergência da série

Determine o intervalo de convergência da série de potências:

Para qual conjunto de valores de , a sequência cujo enésimo termo é definido por

.

converge?

Determine o intervalo de convergência da série:

Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

8)

Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

9)

Encontre uma representação em série de potências para a função e determine o intervalo de convergência.

10)

Encontre uma representação em série de potências para a função e determine o raio de convergência.

16)

Encontre uma representação em série de potências para a função e determine o raio de convergência.

15)

Encontre uma representação em série de potências para a função e determine o raio de convergência.

17)

Encontre uma representação em série de potências para a função e determine o raio de convergência.

19)

Se a série de potências diverge, então é correto afirmar que

1. A série diverge para
2. A série converge para
3. A série converge para
4. A série converge para
5. A série diverge para

Encontre uma representação em série de potências para a função e determine o raio de convergência.

20)

Encontre uma representação em série de potências para a função e determine o raio de convergência.

18)

Encontre o intervalo de convergência da série

Encontre o intervalo de convergência da série

1. Determine o raio de convergência da série de potências .

. Sobre a série de potências podemos afirmar que seu raio de convergência e seu intervalo de convergência são:

Escolha uma opção:

. e

. e

. e

. e

. Converge em todo real

Sabendo que a aproximação de Stirling é

,

calcule o raio de convergência da seguinte série de potências

.

Escreva as seguintes funções como uma série de potências em torno de zero e encontre seu raio de convergência:

1. Seja uma função infinitamente derivável. Suponha que a série de Taylor da centrada em seja dada pela série

1. Determine o raio de convergência desta série

2. Encontre uma representação em série de Maclaurin para a e determine o raio de convergência.

b)

2. Encontre uma representação em série de Maclaurin para a e determine o raio de convergência.

Calcular o raio de convergência da seguinte série de potências

Na resposta, é permitido um erro pra cima ou pra baixo de .

3. Julgue em para os itens corretos e para os errados. Justificando os itens corretos e corrigindo os errados.

c) Se , então o intervalo de convergência da série de potências é

(Capítulo 11.9 – Exercício 25) Calcule a integral indefinida como uma série de potências. Qual é o raio de convergência?

Estude a convergência da série de potências:

(Capítulo 11.9 – Exercício 17) Encontre uma representação em série de potências para a função e determine o raio de convergência.

5 – Determine o raio e o intervalo de convergência absoluta da seguinte série de potências:

1 – Determine a série de Maclaurin da função , assim como o intervalo de convergência absoluta de tal série.

5 – Determine o raio e o intervalo de convergência absoluta da seguinte série de potências:

Determine o intervalo de convergência da série abaixo:

2. Encontre uma representação em série de Maclaurin para a e determine o raio de convergência.

c) , onde

Determine o intervalo de convergência da função

Resolva os seguintes itens sobre séries:

Determine o centro da série de potências e o seu intervalo de convergência

Questão 2 (Justifique todas as suas respostas):

Determine uma série de potências com intervalo de convergência

3. Calcule a integral indefinida como uma série de potências. Qual é o raio de convergência?

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

13 - Determine o raio e o intervalo de convergência das séries:

a)

13 - Determine o raio e o intervalo de convergência das séries:

b)

13 - Determine o raio e o intervalo de convergência das séries:

d)

13 - Determine o raio e o intervalo de convergência das séries:

c)

13 - Determine o raio e o intervalo de convergência das séries:

j)

13 - Determine o raio e o intervalo de convergência das séries:

k)

13 - Determine o raio e o intervalo de convergência das séries:

l)

13 - Determine o raio e o intervalo de convergência das séries:

m)

13 - Determine o raio e o intervalo de convergência das séries:

n)

13 - Determine o raio e o intervalo de convergência das séries:

o)

13 - Determine o raio e o intervalo de convergência das séries:

p)

Determine o intervalo e o raio de convergência da série de potências dada

Determine o intervalo e o raio de convergência da série de potências dada

Determine o intervalo e o raio de convergência da série de potências dada

Determine o intervalo e o raio de convergência da série de potências dada

Determine o intervalo e o raio de convergência da série de potências dada

4. Determine o intervalo e o raio de convergência das séries de potencias a seguir:

f)

4. Determine o intervalo e o raio de convergência das séries de potencias a seguir:

e)

2 – Encontre para quais valores de a série

Converge.

4. Verifique se cada uma das afirmações abaixo é verdadeira ou falsa. Justifique

provando as verdadeiras e apresentando um contra-exemplo para as falsas.

(i) Se uma série de potências converge em um extremo de seu intervalo de convergência e diverge no outro, então a convergência naquele extremo é condicional.

4. Verifique se cada uma das afirmações abaixo é verdadeira ou falsa. Justifique

provando as verdadeiras e apresentando um contra-exemplo para as falsas.

(j) Uma série de potencias pode convergir apenas em dois valores de .

4. Verifique se cada uma das afirmações abaixo é verdadeira ou falsa. Justifique

provando as verdadeiras e apresentando um contra-exemplo para as falsas.

(h) Se uma série de potências é absolutamente convergente em um dos extremos de seu intervalo de convergência, então ela também converge absolutamente no outro extremo.

Determine o intervalo e o raio de convergência das séries de potência a seguir:

Determine o intervalo e o raio de convergência das séries de potência a seguir:

Obtenha representação em série de potências para cada função abaixo e determine o seu intervalo de convergência

3 – Discuta a convergência (diverge ou converge condicionalmente ou converge absolutamente) das séries abaixo:

a)

Determine o intervalo e o raio de convergência da série de potências dada

Determine o raio de convergência e o intervalo de convergência da série de potências

Encontre o intervalo de convergência da série . Não esqueça de testar os extremos do intervalo, se for o caso.

Considere a série de potências

1. Encontre o raio de convergência e o intervalo de convergência da série de potências acima

Determine o intervalo e o raio de convergência das séries de potência a seguir:

O raio de convergência e o intervalor de convergência da série de potências são respectivamente:

Escolha uma opção:

a. e

b. e

c. e

d. e

e. e

f. e