Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.4 - Ex. 4
A função demanda para um pacote de viagem em particular é . Encontre o excedente econômico quando o nível de vendas do pacote é . Ilustre desenhando a curva de demanda e identificando o excedente econômico como uma área.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o excedente econômico quando o nível de vendas for e sabendo que a curva de demanda é dada por.
Para isso, utilizaremos a integral do excedente de produção:
Onde é o preço de venda e é a nossa função. Depois, iremos esboçar a curva de demanda e identificar o excedente como uma área.
Vamos lá!
Passo 2
Como o nosso nível de vendas vai de a , o excedente econômico será dado por:
Então, substituindo a nossa função, temos:
Somando os termos semelhantes do integrando e colocando a constante do lado de fora da integral, ficamos com:
Então, integrando em relação a :
Substituindo os limites de integração, temos:
Simplificando a expressão:
Então o excedente econômico é:
Passo 3
O excedente econômico é a área entre a curva de demanda e a reta que representa a demanda quando o nível de vendas é de , então nossa área pode ser esboçada no gráfico mostrado a seguir:
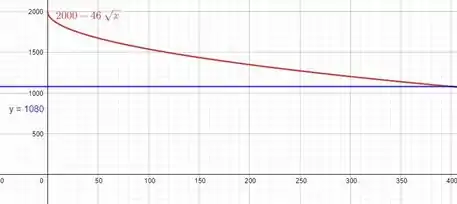
Valeu, galera! Até a próxima! 😉