Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 60
A função de Heaviside definida no Exercício 57 pode também ser usada para definir uma função rampa , que representa o crescimento gradual na voltagem ou corrente do circuito.
(a) Esboce o gráfico da função da rampa .
(b) Esboce o gráfico da voltagem no circuito se uma chave for ligada no instante e a voltagem crescer gradualmente até em um intervalo de segundos. Escreva uma formula para em termos de para .
(c) Esboce o gráfico da voltagem em um circuito se em for ligada uma chave e a voltagem crescer gradualmente até em um período de segundos. Escreva uma fórmula para em termos de para .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos disse que a função de Heaviside pode ser usada para definir uma função rampa , que representa o crescimento gradual na voltagem ou corrente do circuito. Essa função foi definida no exercício 57 da seguinte forma:
Então, ele nos pede para esboçar o gráfico da função rampa e o gráfico da voltagem no circuito em diferentes condições de crescimento da função e diferentes intervalos de tempo.
Pra isso, nós diremos que a função rampa é . Assim, usando a definição da função , vamos apenas multiplicar em cada equação e esboçar seu gráfico. Em seguida, vamos definir por partes, para cada intervalo dado pelo enunciado, e também esboçar seu gráfico.
Vamos lá!
Passo 2
Vamos começar resolvendo a letra (a), esboçando a função rampa definida por . Assim, multiplicando na definição da função , vamos ter:
Isso acontece porque não existe tempo negativo. Então, esboçando o gráfico, temos:
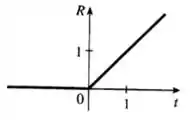
Passo 3
Na letra (b), precisamos esboçar o gráfico da voltagem no circuito se uma chave for ligada no instante e a voltagem crescer gradualmente até em um intervalo de segundos.
Dessa forma, usando a definição do passo , teremos:
Dessa forma, agora a nossa função vai assumir a forma da função rampa.
E como sabemos que em seu valor é volts, vamos usar isso para definir um valor de .
Como , a função vale , portanto:
Daí, vimos que a inclinação da nossa função rampa vai ser .
Observe que a nossa função é .
Então, esboçando o gráfico, teremos:
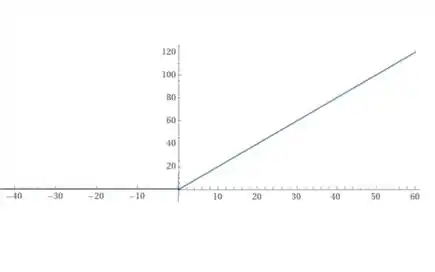
Passo 4
Agora na letra (c), vamos precisar esboçar o gráfico da voltagem em um circuito se em for ligada uma chave e a voltagem crescer gradualmente até em um período de segundos.
Só que antes, precisamos escrever uma fórmula para em termos de para . Nessas condições, usando a definição de , vamos ter:
Para que a função degrau só comece a valer como 1 no tempo , vamos andar com ela para a direita em 7 unidades, para isso, precisamos subtrair no valor do tempo:
Dessa forma, a nossa função vai assumir a forma:
Sendo que a função é logo, , portanto:
E para encontrar a inclinação da rampa, vamos usar do fato de que a é quando , logo,
E como , temos que , logo:
Agora observe que a nossa função é
Então, esboçando o gráfico, temos:
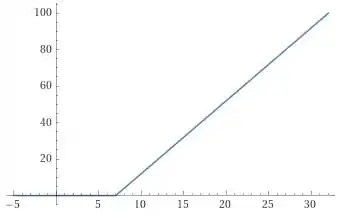
Valeu, galera! Até a próxima! 😉