Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.Revisão - Ex. 74
Uma função importante em Estatística é a função densidade de probabilidade definida por
Onde são constantes tais que e é um número real qualquer. Ache:
- Os extremos relativos de f;
- Os pontos de inflexão do gráfico de f;
- ;
- Faça um esboço do gráfico de f.
Passo 1
Letra (a), para determinar os extremos relativos de uma função devemos achar os valores para os quais ou não existe.
Calculando a derivada:
Para facilitar a compreensão podemos fazer algumas substituições:
Sendo assim:
A derivada de uma função deste tipo é dada como:
Como y é dado em função da variável x, usamos a Regra da Cadeia:
Derivando y:
Então:
Igualando a 0
Quando a função terá um extremo relativo.
Passo 2
Letra (b), para saber se o gráfico possui ponto de inflexão devemos calcular os valores para os quais ou não existe.
Para derivar usamos a Regra da Cadeia:
Igualando a 0:
Reorganizando
Resolvendo:
Quando o valor de e, consequentemente, não há valor real para x. Quando , e os pontos de inflexão serão:
Passo 3
Letra (c),
A função é divergente.
Na letra (c):
A função é divergente.
Passo 4
Na Letra (d), para esboçar o gráfico podemos assumir valores aleatórios para
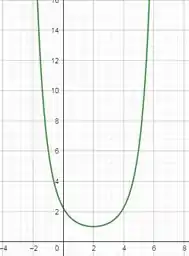
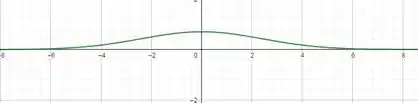
Resposta
- Extremos relativos:
- Quando os pontos de inflexão são: ,
- ;
Quando não há pontos de inflexão;