As funções a seguir definem campos vetoriais em . Determinar e fazer os gráficos das curvas onde tem direção constante.
b) ;
Passo 1
Bom galera, o que faremos aqui?
Para achar o gráfico de y versus x nós precisamos achar o y em relação ao x, certo?
As funções irão formar um ângulo entre o gráfico e o eixo x.
Então nós podemos assumir que:
Lembrando que:
Como:
Substituindo:
Se:
Se imaginarmos o triângulo retângulo formado pela reta e pelo eixo x:
Reorganizando:
Agora que já sabemos isso podemos começar !!
Passo 2
Para a letra (b):
Substituindo na fórmula do Passo 1:
Então, nós teremos uma família de parábolas que também passam pelo ponto (0,0).
Desenhando:
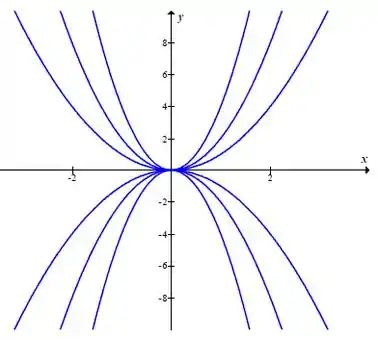
Tranquilinha?
Resposta
Ei, a resposta está no passo a passo :)