Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 21

Use a definição 2 para achar uma expressão para a área sob o gráfico de f como um limite. Não calcule o limite.

f x = 2 x x 2 + 1   ,   1 ≤ x ≤ 3 .

Passo 1

Fala, galera! Beleza? O enunciado nos deu a função

f x = 2 x x 2 + 1 ,

definida no intervalo [ 1 ,   3 ] , e pediu pra gente encontrar uma expressão para a área sob o gráfico dela como um limite, usando a definição 2 .

Relembrando (definição 2): para achar a área sob o gráfico de uma função contínua f entre os pontos a e b , aproximamos a região abaixo do gráfico de f utilizando retângulos finos.

Quanto mais retângulos usamos, menores eles são e mais preciso é o valor obtido para a área da região em questão. No limite, com infinitos retângulos beeeeeeeem finos, essa soma dá a área exata sob a curva, que é a integral definida.

Para facilitar as contas, vamos colocar essas ideias em termos matemáticos!

A área A da região S que está sob o gráfico de uma função contínua f é o limite da soma das áreas dos retângulos aproximantes R n , ou seja:

A = lim n → ∞ ⁡   R n =     l i m n → ∞   f x 1 Δ x + f x 2 Δ x + ⋯ + f x n Δ x ,

onde Δ x = b - a n .

Então, para resolvermos a questão precisamos fazer os seguintes passos:

  • Encontrar o valor de Δ x para o intervalo do problema, [ 1 ,   3 ] .
  • Encontrar os pontos x i extremos de cada faixa no eixo x , associada a largura do retângulo aproximante R i .
  • Encontrar os valores de f x i .
  • Expressar a área sob o gráfico de f como um limite, usando a definição 2 .

Bora começar? 😊

Passo 2

A função f está definida no intervalo [ 1 ,   3 ] , então a região S (região azul) que está sob o gráfico de f é limitada pelo gráfico da função e pelas retas verticais x = 1 e x = 3 .

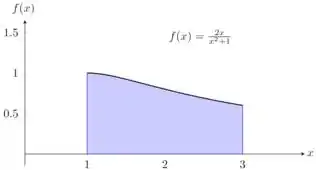
Assim, vale que a = 1 e b = 3 e vamos ter que o comprimento é:

Δ x = 3 - 1 n = 2 n .

Passo 3

Os extremos de cada subintervalo são os pontos

x i = 1 + i   Δ x = 1 + 2 i n ,   para   i = 0 ,   1 ,   2 , … , n .

Sabe por quê? Pensa assim: A partir do primeiro número do intervalo [ 1 ,   3 ] , “andamos” i vezes o comprimento Δ x = 2 n e chegamos ao fim do subintervalo i .

Passo 4

Agora, avaliando a função f x = 2 x x 2 + 1 no ponto x i obtido no passo anterior, temos:

f x i = 2 1 + 2 i n 1 + 2 i n 2 + 1 .

Passo 5

Agora só precisamos encontrar a área de S usando a fórmula apresentada no Passo 1.

Como

A = lim n → ∞ ⁡   R n =     l i m n → ∞   f x 1 Δ x + f x 2 Δ x + ⋯ + f x n Δ x ,

Então substituindo os valores que encontramos na fórmula:

    l i m n → ∞     ∑ i = 0 n   f x i Δ x =   l i m n → ∞     ∑ i = 0 n 2 1 + 2 i n 1 + 2 i n 2 + 1 ⋅ 2 n

E encontramos a expressão para a área sob o gráfico de f como um limite. Como não precisa calcular o limite, essa é a nossa resposta final.

Valeu, galera! Até a próxima! 😉

Resposta

A = l i m n → ∞     ∑ i = 0 n 2 1 + 2 i n 1 + 2 i n 2 + 1 ⋅ 2 n

É uma expressão para a área sob o gráfico de f como um limite, obtida a partir da definição 2 descrita abaixo.

A área A da região S que está sob o gráfico de uma função contínua f é o limite da soma das áreas dos retângulos aproximantes R n :

A = lim n → ∞ ⁡   R n =     l i m n → ∞   f x 1 Δ x + f x 2 Δ x + ⋯ + f x n Δ x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a definição 2 para achar uma expressão para a área sob o gráfico de f como um limite. Não calcule o limite. f x = sin ⁡ x ,0 ≤ x ≤ π
Use a definição 2 para achar uma expressão para a área sob o gráfico de f como um limite. Não calcule o limite. f x = x 2 +1 + 2 x ,4 ≤ x ≤ 7
Seja A área sob o gráfico de uma função contínua crescente f de a até b , e sejam L n e R n as aproximações para A , com n subintervalos usando extremidades esquerdas e direitas, respectivamente. Como
b) Encontre novas estimativas usando 8 retângulos.