Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.1 - Ex. 10
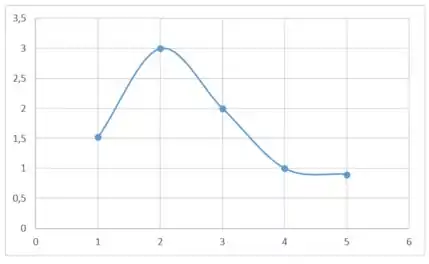
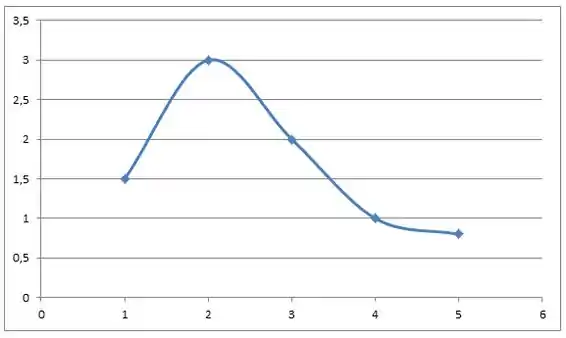
Encontre o gráfico da função f contínua no intervalo [1, 5] com as seguintes propriedades.
Máximo absoluto em 2, mínimo absoluto em 5 e o ponto 4 é crítico, mas sem ser mínimo ou máximo local.
Passo 1
Opaa, esse enunciado traz um desafio pra a gente!
Temos os seguintes dados:
- A função é contínua no intervalo ;
- Máximo absoluto em
- Mínimo absoluto em
- O ponto 4 é crítico, mas sem ser mínimo ou máximo local.
Passo 2
Segundo as informações que o enunciado deu, vamos precisar usar valores de arbitários.
Sabemos que entre e a função cresce, e depois decresce até chegar em , então podemos desenhar:
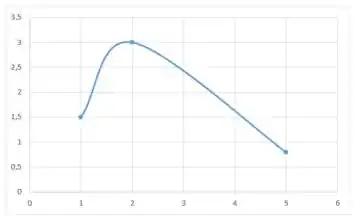
O ponto será só um ponto intermediário e em a gente deve ter um ponto crítico mas ele não deve ser nem um máximo nem um mínimo. Portanto a função que esta decrescendo vai continuar assim, só que em uma taxa menor:
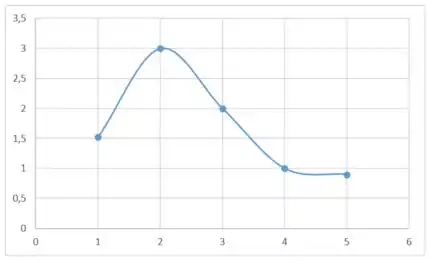
Prontinhoo!
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico de uma função f que seja contínua em [ 1,5 ] e tenha as propriedades dadas:Máximo absoluto em 3 , mínimo absoluto em 2 e mínimo local em 4 .
Esboce o gráfico de uma função f que seja contínua em [ 1,5 ] e tenha as propriedades dadas:Máximo absoluto em 5 , mínimo absoluto em 1 , máximo local em 2 e mínimo local em 4 .
Explique a diferença entre mínimo local e mínimo absoluto.
Esboce o gráfico de uma função f que seja contínua em [ 1,5 ] e tenha as propriedades dadas: f não tem máximos e mínimos locais, mas 2 e 4 são números críticos.
Para cada um dos números a , b , c , d , r e s , diga se a função cujo gráfico é dado tem um máximo ou mínimo absoluto, um máximo ou mínimo local, ou nem máximo, nem mínimo.