Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 35
O gráfico dado mostra a temperatura em em Davis, Califórnia, em 18 de abril de 2008, entre 6 horas e 18 horas.
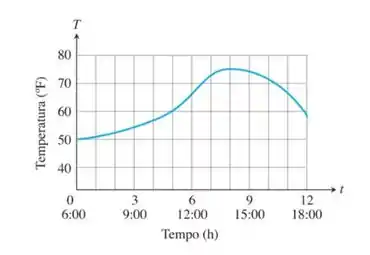
- Estime a taxa de variação da temperatura nos horários
- 7:00
- 9:00
- 14:00
- 16:00
- Em qual horário a temperatura aumenta mais rapidamente? E em qual diminui mais rapidamente? Qual é a taxa para cada um desses horários?
- Trace o gráfico da derivada da temperatura T versus tempo t.
Passo 1
Resolvendo o item (a)
Primeiro, para estimar a taxa de variação da temperatura, devemos esboçar as retas tangentes aos pontos desejados da seguinte maneira:
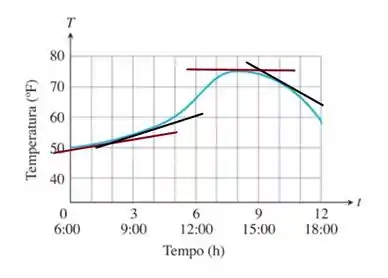
Passo 2
Observando as retas tangentes, devemos lembrar que a taxa de variação de uma função é o mesmo que o coeficiente angular dela.
Calculando o coeficiente angular em cada ponto:
Passo 3
Resolvendo o item (b)
Para saber em qual horário a temperatura cresce mais rapidamente, basta observar qual parte do gráfico está mais inclinada, quanto maior a inclinação, maior a taxa de variação. Assim, podemos afirmar que às 12hrs a temperatura cresce mais rapidamente. Observando a maior inclinação decrescente, temos horário no qual a temperatura cai mais rapidamente, o qual corresponde a 18hrs.
Passo 4
Para esboçar o graficamente a derivada devemos usar os coeficientes angulares da reta tangente a intervalos frequentes, registrando os pares e unindo eles com uma curva suave.
Como já calculamos anteriormente alguns coeficientes angulares, basta, agora, calcular para e para
Ligando os pares encontrados no item (a) e nesse item, temos o seguinte gráfico:
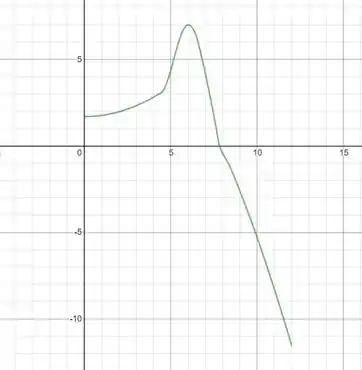
Resposta
Ei, a resposta está no passo a passo :)