Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 60
Faça o gráfico de em uma janela que contenha , . Em seguida, na mesma tela, faça o gráfico de
para . Então tente . Explique o que ocorre.
Passo 1
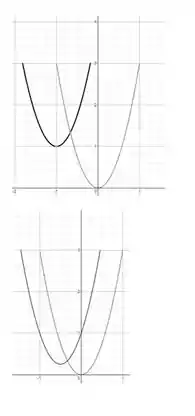
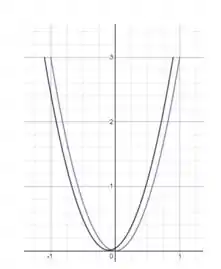
Passo 2
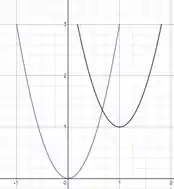
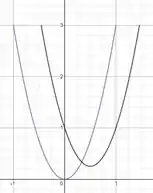
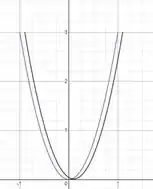
Passo 3
Podemos notar que é a derivada de . Logo quando aproximamos de zero, temos:
Por isso, o gráfico tende a sobrepor a curva de
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule F ' x onde F x é igual a x 2 - 1 x + 1
Calcule F ' x onde F x é igual a x + x 4 x 2 + 3
Calcule f ' x onde f x é igual a x + sen x x - cos x
Calcule F ' x onde F x é igual a x x 2 + 1
Calcule f ' x onde f x é igual a x cos s ec x