- Use as informações a seguir para fazer o gráfico da função f no intervalo fechado .
- O gráfico de é composto por segmentos de reta fechados unidos pelas extremidades
- O gráfico começa no ponto
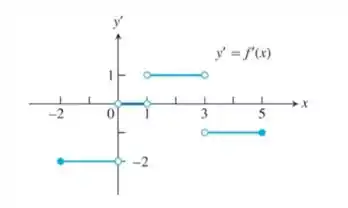
- A derivada de é a função escada da figura a seguir
- Repita o item (a), considerando que o gráfico começa em em vez de .
- O gráfico de é composto por segmentos de reta fechados unidos pelas extremidades
- O gráfico começa no ponto
- A derivada de é a função escada da figura a seguir
Passo 1
Resolvendo o item (a)
Primeiro, devemos observar que o gráfico da derivada é composto por 4 segmentos de reta, o que significa que o gráfico de também é formado por 4 segmentos de reta com as mesmas extremidades dos segmentos da derivada.
Passo 2
Sabendo o ponto de início, é possível afirmar que o primeiro segmento de reta liga o ponto ao eixo no ponto
Para descobrir a coordenada y, basta calcular o coeficiente angular (derivada) do segmento de reta do gráfico de
Passo 3
Observando que entre os pontos e do gráfico de a derivada é nula, podemos afirmar que a função nesses pontos é constante e representada por um segmento de reta entre os pontos e .
Passo 4
No intervalo , a função tem coeficiente angular igual a 1. Logo, sabendo que o terceiro segmento de reta começa no ponto , o próximo ponto pode ser definido fazendo a seguinte relação:
Passo 5
Por fim, basta ligar o ponto ao ponto . Sabendo que a derivada nesse intervalo é , podemos fazer a seguinte relação:
Passo 6
Analisando os passos anteriores, é possível traçar o gráfico de ligando os pontos encontrados da seguinte forma:
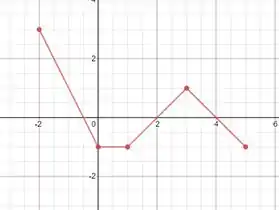
Passo 7
Resolvendo o item (b)
Note que, alterando apenas o ponto inicial, a função continuará com o mesmo padrão da função do item (a). Logo, podemos concluir que, começando em , todo o gráfico cairá 3 unidades no eixo .
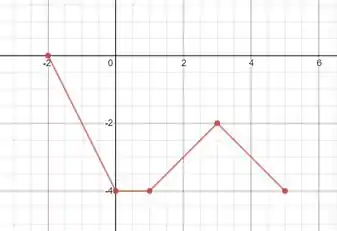
Resposta
Ei, a resposta está no passo a passo :)