Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 92

Seja

a) Mostre que é contínua em .

b) Pesquise graficamente se é derivável em por meio de sucessivos zooms em direção ao ponto no gráfico de .

c) Mostre que não é derivável em .

Passo 1

E aí! como vai?

Nesse problema foi dada a função

E nosso objetivo é mostrar que é contínua em e que não é derivável nesse ponto. Além disso vamos usar uma ferramenta gráfica para observar a função no ponto .

Tem ideia de como fazemos isso?

Perceba que a função é definida por partes justamente em , então para que a função seja contínua a parte tem que tender a nos dois lados.

E para mostrar que não é derivável em , vamos tentar aplicar a definição

Bora lá!

Passo 2

Para que a função seja contínua em um ponto, o valor da função neste ponto deve coincidir com o valor do limite. Note que . Para tomarmos o limite quando , devemos tomar , de modo que . Assim,

Vamos simplificar a função do limite aplicando as propriedades logarítmicas e ...

Desta forma, o limite que demos calcular é

Este limite é indeterminado do tipo . Assim, aplicando a regra de L’Hospital:

A regra de L’Hopital consiste em calcular a derivada do numerador e do denominador separadamente e substituir no limite...

Pelo teorema fundamental do calculo, temos

Pela regra da potencia...

Substituindo no limite

Fazemos separar em limites laterais, temos que para :

Para temos que

Como os limites laterais são iguais,

Desta forma,

Portanto é contínua em .

Tranquilo até aqui?

Passo 3

Fazendo sucessivos zooms no gráfico da função usando uma ferramenta grafica, ela aparenta ser derivável em :

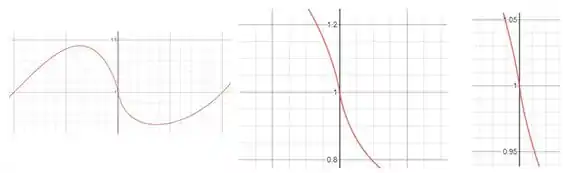
Concorda?

Passo 4

Vimos que a função aparenta ser derivável em , porém agora vamos mostrar que ela não é!!!

Vamos tentar calcular pela definição:

Como , o limite é indeterminado do tipo 0/0.

Vamos aplicar a regra de L’Hospital. A derivada do numerador será

Aplicando aquelas propriedades logarítmicas que usamos no passo anterior...

Por outro lado:

Assim, a derivada do numerador é

Desta forma, como o denominador é apenas

Substituindo no limite

Quando tende a pela direita, , ou seja

Agora quando tende a pela esquerda, ...

Perceba que o limite divergiu, logo não existe!

Por isso, não é derivável em pois tem tangente vertical nesse ponto (por isso parecia que ela era derivável: ela é suave e admite reta tangente, mas a tangente é vertical).