Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 31
- O gráfico da figura a seguir é composto por segmentos de reta unidos pelas extremidades. Em quais pontos do intervalo [- 4, 6] a função não é definida? Justifique sua resposta
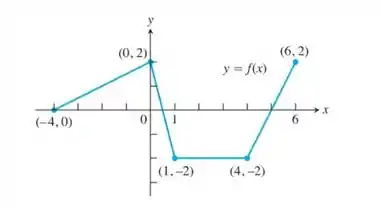
- Desenhe o gráfico da derivada de. O gráfico deve mostrar uma função escada.
Passo 1
Resolvendo o item (a)
Devemos lembrar que a derivada é o coeficiente angular da reta tangente ao gráfico. Logo, observando o gráfico, é possível notar que não há como definir uma reta tangente nos pontos , ( e . A funções em cada lado desses pontos são funções diferentes; por isso, não há como definir qual a angulação da reta tangente e, consequentemente, não se tem uma função definida.
Passo 2
Resolvendo o item (b)
Como a função é composta por retas, devemos notar que os coeficientes angulares das retas tangentes coincidem com os coeficientes angulares da própria função.
Portanto,
no intervalo
No intervalo
No intervalo
, pois a função é constante
No intervalo
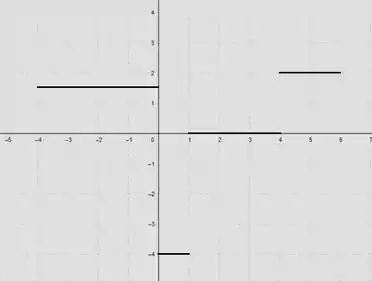
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Coeficientes angulares no gráfico da função tangente: Esboce em apenas um gráfico y = t g( x ) e sua derivada em ( - π / 2 ,π / 2 ) . O gráfico da função tangente parece ter um coeficiente angular mín
Explorando ( s e nk x ) / x : Esboce em um único gráfico y = ( s e nx ) / x , y = ( s e n2 x ) / x e y = ( s e n4 x ) / x no intervalo - 2 ≤ x ≤ 2 . Onde cada gráfico parece cruzar o eixo y ? Os gráfi
Radianos versus graus: derivadas no modo grau. O que aconteceria com as derivadas de sen x e cos x se x fosse medido em graus em vez de radianos? Para descobrir isso, siga os seguintes passos:Sele
Precaução com o quociente da diferença centrada (Continuação do Exercício 65). O quociente f x + h - f ( x - h ) 2 h Pode ter um limite h → 0 quando f não possui derivada em x . Para exemplificar, con
Radianos versus graus: derivadas no modo grau. O que aconteceria com as derivadas de sen x e cos x se x fosse medido em graus em vez de radianos? Para descobrir isso, siga os seguintes passos:Sele