Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 70b
Radianos versus graus: derivadas no modo grau. O que aconteceria com as derivadas de e se fosse medido em graus em vez de radianos? Para descobrir isso, siga os seguintes passos:
- Selecione o modo grau da calculadora gráfica ou computador e faça o gráfico de
- Ainda no modo grau da calculadora gráfica, estime
- Agora volte para a dedução da fórmula para a derivada de no texto e siga os passos da derivação usando limites no modo grau. Que fórmula você obtém para a derivada?
- Agora volte para a dedução da fórmula para a derivada de no texto e siga os passos da derivação usando limites no modo grau. Que fórmula você obtém para a derivada?
- As desvantagens das fórmulas no modo grau se tornam evidentes quando você começa a lidar com derivadas de ordem superior. Tente. No modo grau, quais são a segunda e terceira derivadas de e ?
E estime . Compare sua estimativa com . Existe alguma razão para acreditar que o limite deveria ser ?
Passo 1
Questões com muito texto pode nos confundir. Vamos começar por determinar o que precisamos fazer exatamente em cada letra.
- Vamos obter o gráfico de , calcular o valor de e comparar com ;
- Vamos calcular o limite da função dada;
- Derivar pela definição a função ;
- Mesmo procedimento do passo anterior, mas pra ;
- Obter a segunda e terceira derivada de e .
Passo 2
Vamos calcular agora o seguinte limite:
Para isto, temos a seguinte tabela:
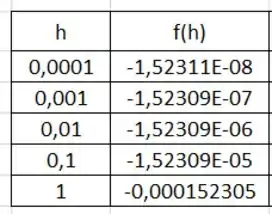
Como pode ser observado na tabela, quando , o valor da nossa função também tende a 0. Desta forma, tanto faz o modo grau quando radiano, em ambos os casos a função possui o mesmo comportamento.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. G t = 4 t t + 1
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. g t = 1 t
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. g x = 1 + 2 x
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. f x = 3 + x 1 - 3 x
Encontre a derivada da função dada usando a definição. Diga quais são os domínios da função e da derivada. f x = 1,5 x 2 - x + 3,7