Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 34
O gráfico da função é mostrado a seguir. Em que pontos as seguintes sentenças são verdadeiras?
a) e são ambas positivas.
b) e são ambas negativas.
c) é negativa, mas é positiva.
Passo 1
Antes de começar o exercício, devemos lembrar que a primeira derivada indica se a função está crescendo (se for positiva) ou decrescendo (se for negativa). Já a segunda derivada indica se a concavidade é para cima (se for positiva) ou para baixo (se for negativa).
Nos é dado o seguinte gráfico
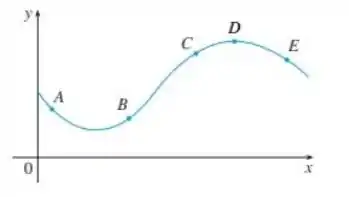
E temos que avaliar em quais pontos as afirmações dadas são verdadeiras.
Passo 2
Podemos analisar a letra a).
a) e são ambas positivas.
Então precisamos que a função seja crescente e que a concavidade dela seja voltada para cima, temos essas duas condições atendidas para o ponto B.
Passo 3
Agora vamos analisar a letra b).
b) e são ambas negativas.
Aqui precisamos que a função seja decrescente e que sua concavidade seja voltada para baixo, temos essas duas condições atendidas no ponto E.
Passo 4
Já na letra c)
c) é negativa, mas é positiva.
Precisamos que a função seja decrescente, mas que sua concavidade seja voltada para cima, e essas duas condições estão presentes no ponto A.