Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 42
(a) O gráfico de uma função posição de um carro é mostrado onde é medido em pés e , em segundos. Use-o para fazer o gráfico da velocidade e da aceleração do carro. Qual é a aceleração em segundos?
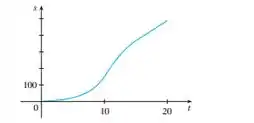
(b) Use a curva da aceleração da parte (a) para estimar o arranco em segundos. Quais são as unidades para o arranco?
Passo 1
E aí! tudo certinho?
Nesse problema foi dado o gráfico da função posição de um carro e nosso objetivo é determinar o gráfico da velocidade , da aceleração e estimar a aceleração e o arranco do carro em .
Parece complicado?
O gráfico que foi dado da posição é
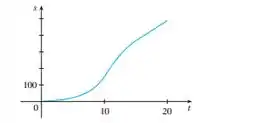
Dos princípios físicos, sabemos que a velocidade é dada por
E a aceleração é dada por
Já o arranco, que vamos chamar de , é dado por
Para esboçar os gráficos, temos que lembrar que a derivada de uma função pode ser interpretada como as inclinações das retas tangentes da função em cada ponto do seu domínio.
Veja só!
Passo 2
Vamos começar fazendo o gráfico para representar a velocidade e a aceleração.
Começando pela função , vemos que a função inicialmente possui uma inclinação positiva e crescente enquanto a partir de podemos ver que sua inclinação continua positiva, porém menos crescente.
Assim podemos esboçar o gráfico da velocidade como
Agora esboçando o gráfico da aceleração , vamos fazer a mesma análise, mas agora para ...
Inicialmente a função é crescente e quando chega em , a função possui inclinação já que a reta tangente a esse ponto é horizontal. A partir daí vamos que a função começa a decrescer e permanece constante a partir de certo ponto.
Assim, a função aceleração pode ser esboçada como
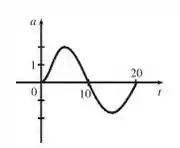
Tranquilo até aqui?
Passo 3
Para a letra (b), ao desenhar uma linha tangente em no gráfico da aceleração, esta parece diminuir em durante um período de , como podemos observar.
Então, em , o arranco é aproximadamente .
Se , possui unidade e como é em , temos
Sacou? O que achou? Responde Aí!
Resposta
- a aceleração é em .
- o arranco é aproximadamente .