Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.4 - Ex. 7
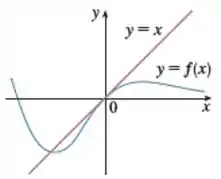
O gráfico da função e sua reta tangente em 0 estão exibidos abaixo. Qual é o valor de ?
Passo 1
O enunciado nos apresenta o gráfico de e pede para determinarmos
Primeiramente, vamos chamar
Desta maneira, teremos um limite da seguinte forma
Queremos saber o valor do limite quando .
Através do gráfico dado, vemos que o limite da função quando . O limite da função também tenderá à zero uma vez que quando .
Logo, temos uma forma indeterminada do tipo .
O melhor jeito de resolver limites que apresentam essa forma é através da Regra de l’Hôspital.
Passo 2
Sabemos que na Regra de l’Hôspital temos que
e para que o limite exista.
No passo anterior, definimos que , logo
Portanto, está dentro das condições da Regra.
Porém, quem será se não nos foi dado o valor de ? Sabemos que a derivada de uma função em um dado ponto é igual ao coeficiente angular da reta tangente à esta curva da função no ponto .
Ao olhar o gráfico dado pelo enunciado, vemos que a reta é tangente a função no ponto , portanto o seu coeficiente angular será igual ao coeficiente angular de neste ponto. Como o coeficiente de é igual a constante 1 em , temos que
neste mesmo ponto.
Aplicando a Regra de l’Hôspital, obtemos