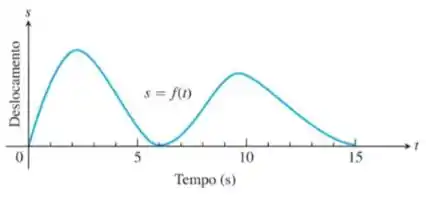
O gráfico mostra a posição de um corpo que se desloca para cima e para baixo sobre uma reta coordenada.
- Quando o corpo se afasta da origem? E quando ele se aproxima dela? Em que instantes, aproximadamente, a partícula apresenta (b) velocidade igual a zero? (c) E aceleração igual a zero? (d) Quando a aceleração é positiva? E negativa?
Passo 1
- Quando o corpo se afasta da origem? E quando ele se aproxima dela?
- Em que instantes, aproximadamente, a partícula apresenta velocidade igual a zero?
- Em que instantes, aproximadamente, a partícula apresenta aceleração igual a zero?
- Quando a aceleração é positiva? E negativa?
O corpo se afasta da origem quando a função de está crescendo, ou seja, nos intervalos de aproximadamente: e .
O corpo se aproxima da origem quando a função de está decrescendo, ou seja, nos intervalos de aproximadamente: e .
Passo 2
A velocidade vai ser zero, quando a derivada primeira da função for zero, ou seja nos pontos críticos de gráfico. São eles: .
Passo 3
A aceleração vai ser zero quando a derivada segunda da função for zero, ou seja nos pontos onde a concavidade muda.
São eles:
Passo 4
A aceleração é positiva quando a concavidade é para cima, os seja nos instantes e .
A aceleração é negativa quando a concavidade da função é para baixo, nos instantes e .
Resposta
- e .
- e .
e
e .