Suponhamos que a derivada da função seja .

Em que pontos, se houver, o gráfico de f apresenta um mínimo local, um máximo local, ou um ponto de inflexão? (Dica: desenhe o padrão de sinais de y'.)

Vamos calcular a derivada segunda então...

Substituindo os valores nessa função então, temos:

Sobre ainda não podemos afirmar nada pois foi nula. Mas já sabemos que temos um mínimo local em .

Os pontos de inflexão são quando a derivada segunda é zero. Nossa é:

Resolvendo a equação do segundo grau, temos: .

Vamos então fazer a tabela de sinais de e para definir os intervalos de crescimento e o tipo de concavidade:

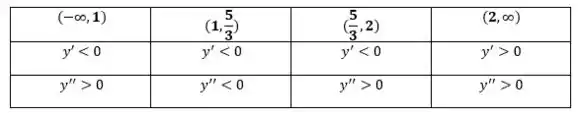
Então, temos pontos de inflexão em e .