Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 57

Um modelo para dispersão de um rumor é dado pela equação

p t = 1 1 + a e - k t

Onde p ( t ) é a proporção da população que já ouviu o boato no tempo t e a e k são constantes positivas.

  1. Quando a metade da população terá ouvido um rumor?
  2. Quando ocorre a maior taxa de dispersão do boato?
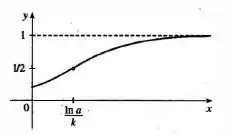
  3. Esboce o gráfico de p

Passo 1

  1. Como p ( t ) é a proporção da população que já ouviu o rumor, metade ter ouvido significa p t = 1 2 . Substituindo na equação e isolando t , temos que:

    2. 1 2 = 1 1 + a e - k t ⇒ 1 + a e - k t = 2 ⇒ a e - k t = 1 ⇒ e - k t = 1 a ⇒ ln ⁡ e - k t = ln ⁡ 1 a

    ⇒   - k t = ln ⁡ 1 a ⇒ t =   - 1 k ln ⁡ 1 a ⇒ t = - 1 k ln ⁡ a - 1 ⇒ t = ln ⁡ a k

    Logo no tempo t = ln ⁡ a k é quando metade da população terá ouvido o rumor.

    Passo 2

  2. Para sabermos a maior taxa de dispersão devemos aplicar o teste da derivada. Assim temos que:

    3. p ' t = a k e - k t 1 + a e - k t 2 ⇒ p ' ' t = a k 2 e - k t a e - k t - 1 1 + a e - k t 3

    Por consequência:

    p ' ' t > 0 ⇒ a e - k t > 1 ⇒ - ln ⁡ e - k t > ln ⁡ 1 a ⇒ - k t > ln ⁡ a - 1 ⇒ t > ln ⁡ a k

    Logo o tempo em que ocorre a maior taxa de dispersão do boato é quando metade da população ouve como calculado em (a), t = ln ⁡ a k .

    Passo 3

  3. Definimos dois aspectos importantes do gráfico primeiro, onde ele cruza o eixo x   e se possui assíntota . Assim:

p 0 = 1 1 + a e - k 0 = 1 1 + a

E

lim t → ∞ ⁡ 1 1 + a e - k t = lim t → ∞ ⁡ 1 1 + a e k t = 1

Então o gráfico é dado por:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se f for a função do Exercício 14, encontre f e f ' ' e use seus gráficos para estimar os intervalos de crescimento e decrescimento e de concavidade de f . f x = 2 x + 3 2 x - 2 5 x 3 x - 5 2
a) Faça o gráfico da funçãob) Explique a forma do gráfico calculando o limite quando x → 0 + ou quando x → ∞ .c) Estime os valores máximo e mínimo e então use o cálculo para achar os valores exatos.d)
Sef for a função considerada no Exemplo 3, use um sistema de computação algébrica para calcularf ' então faça seu gráfico para confirmar que todos os valores máximos e mínimos são como dados no exempl
a) Faça o gráfico da funçãob) Explique a forma do gráfico calculando o limite quando x → 0 + ou quando x → ∞ .c) Estime os valores máximo e mínimo e então use o cálculo para achar os valores exatos.d)
Descreva a mudança no gráfico de f à medida que c varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos